Предмет: Алгебра,
автор: cop88
помогите пожалуйста
Приложения:
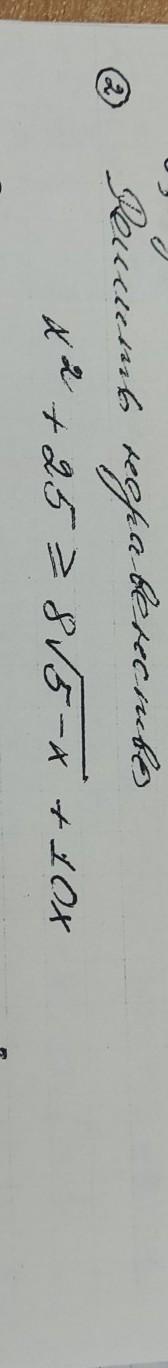
Ответы
Автор ответа:
1
Объяснение:
ОДЗ: 5-х≥0 х≤5 ⇒ х∈(-∞;5].
-∞__+__1__-__5__+__+∞ ⇒
x∈(-∞;1]U[5;+∞).
Учитывая ОДЗ:
Ответ: х∈(-∞;1]U[5].
Похожие вопросы
Предмет: Английский язык,
автор: lerusia3055
Предмет: Русский язык,
автор: KolegovT
Предмет: Английский язык,
автор: Мандаринка201612
Предмет: Математика,
автор: Данил12312
Предмет: Биология,
автор: bkmzbkmzmir