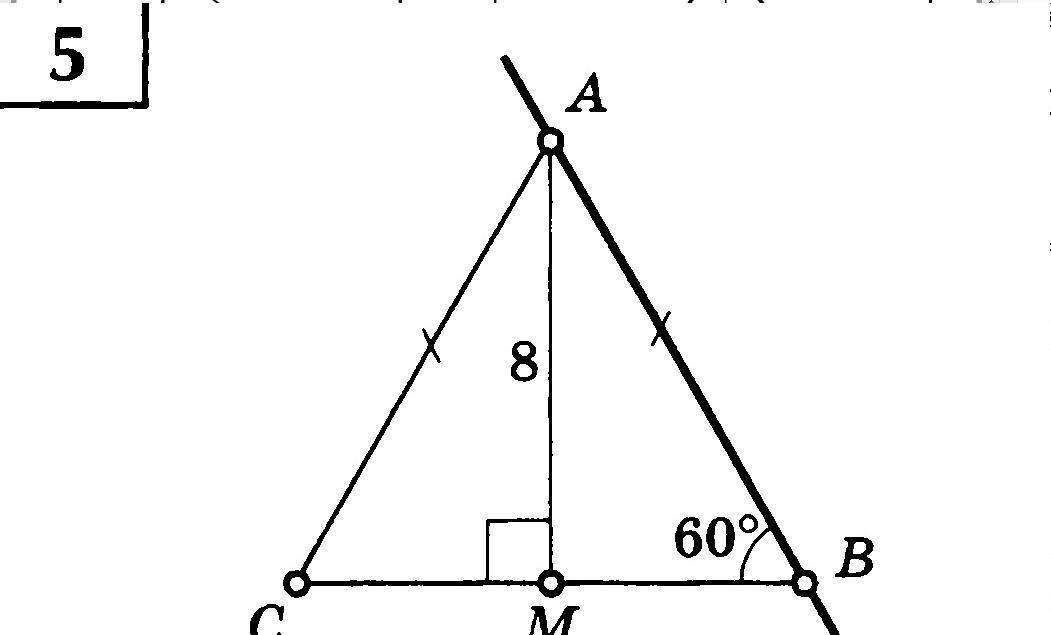
найти расстояние от точки М до прямой АВ
Ответы
Ответ:
4
Объяснение:
т.к. дан равносторонний треугольник, что следует из того что АС=АВ, значит. углы С и В равны как углы при основании равнобедренного треугольника, но они равны по 60°, а сумма углов треугольника равна 180°, получается, что и угол А равен 60° т.е. треугольник равносторонний, в нем высота АМ= 8 см, и т.к. она равна АВ√3/2, то сторона в этом треугольника находится из условия АВ√3/2=8, значит, АВ=16*/√3=16√3/3, МВ=АВ/2=8√3/3, т.к. это катет, лежащий против угла в 30° в прямоугольном треугольнике АВМ, , используя свойства пропорциональных отрезков в прямоугольном треугольнике АМВ, находим проекцию МВ на гипотенузу из условия
МВ²=АВ*х, где х- искомая проекция,
х=МВ²/АВ=(64*3/9):(16√3/3)=4√3/3; тогда высота, проведенная к стороне АВ- это искомое расстояние- может быть найдена из условия
h²=х*(АВ-х), h²=(4√3/3)*(16√3/3-4√3/3)= (4√3*12*√3)/(3*3)=16
откуда h=√16=4