Предмет: Алгебра,
автор: rockyhog1337
ПОМОГИТЕ С АЛГЕБРОЙ! ДАЮ 100 БАЛЛОВ!
Приложения:
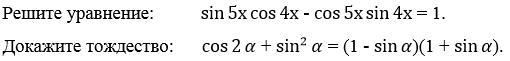
Ответы
Автор ответа:
2
1) sin5xcos4x - cos5xsin4x = 1
sin(5x-4x) = 1
sinx= 1
x = π/2 + 2πn
2) (cos2a = 1-2sina^2)
1-2sina^2 + sina^2 = 1-sina^2
1-sina^2 = 1-sina^2
Автор ответа:
0
Ответ:
Применяем формулу синуса разности.
Применяем формулу косинуса двойного угла и разности квадратов.
Тождество доказано .
Похожие вопросы
Предмет: Українська мова,
автор: svp80
Предмет: Русский язык,
автор: seginutik
Предмет: Русский язык,
автор: Настя4595
Предмет: Қазақ тiлi,
автор: olivebrooklyn
Предмет: Українська мова,
автор: sretu