Question

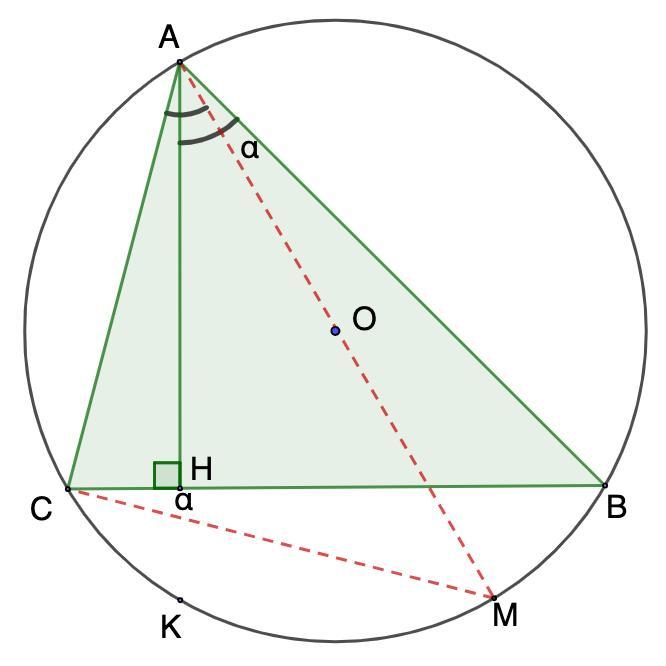
Доведіть, що в трикутнику АВС кут ОАС дорівнює куту BAH, де О - центр описаного кола, Н - основа висоти, проведеної з вершини А.

Answer 1

Ответ:

Доказано, что угол ОАС равен углу BAH.

Объяснение:

Докажите, что в треугольнике АВС угол ОАС равен углу BAH, где О - центр описанного круга, Н - основа высоты, проведенной из вершины А.

Дано: ΔАВС;

АН - высота;

Окр.О - описанная.

Доказать: ∠ОАС = ∠BAH.

Доказательство:

1. Пусть ∠МАВ = α

• Вписанные углы, опирающиеся на одну дугу, равны.

⇒ ∠МСВ = ∠МАВ = α. (опираются на ◡МВ)

• Вписанный угол, опирающийся на диаметр, равен 90°.

⇒ МСА = 90°

Тогда ∠АСВ = 90° - α

2. Рассмотрим ΔСАН - прямоугольный.

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠САН = 90° - ∠АСВ = 90° - (90° - α) = α

3. ∠ОАС = α + ∠НАМ

   ∠BAH = α + ∠НАМ

• Если правые части равенств равны, то равны и левые.

⇒ ∠ОАС  = ∠НАМ