Задание приложено...
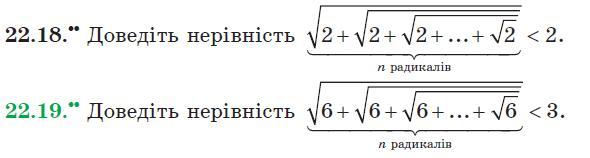
Ответы
Ответ:
Метод математической индукции:
Для того, чтобы доказать, что некоторое утверждение верно при натуральном необходимо выполнить следующие условия:
База индукции:
- 1) Доказать, что утверждение верно при
Индуктивный переход:
- 2) Сделать гипотезу, что утверждение верно для
и на основании данной гипотезы доказать, что утверждение верно для
Если выполнены утверждения 1) и 2), то исходное утверждение доказано для всех натуральных методом математической индукции.
22.18
Воспользуемся методом математической индукции:
База индукции:
- верно
Индуктивный переход:
- пусть верно
Необходимо доказать:
Так как по индуктивному предположению , то усилим неравенство для
заменим вложенные корни числом 2, так как по индуктивному предположению 2 больше чем
вложенных корней.
Так как все таки для вложенных корней меньше чем 2, то сумма
2 + 2 = 4 меньше чем 4, то есть корень чуть меньше. Разницу между запишем с помощью при
- верно
22.19
Воспользуемся методом математической индукции:
База индукции:
- верно
Индуктивный переход:
- пусть верно
Необходимо доказать:
Так как по индуктивному предположению , то усилим неравенство для
заменим вложенные корни числом 3, так как по индуктивному предположению 3 больше чем
вложенных корней.
Так как все таки для вложенных корней меньше чем 3, то сумма
6 + 3 = 9 меньше чем 9, то есть корень чуть меньше. Разницу между запишем с помощью при
- верно