Предмет: Алгебра,
автор: quickruler
Методом непосредственного интегрирования найти
Приложения:
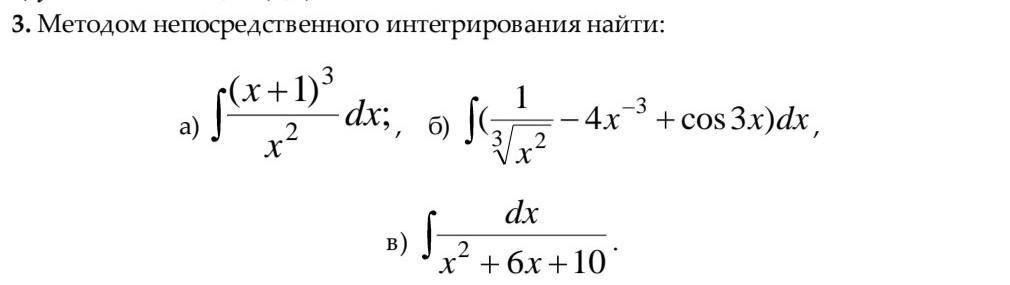
sangers1959:
Ещё нужно решение примеров?
да
скинь решение пж
Ответы
Автор ответа:
1
Объяснение:
a)
б)
в)
есть тг?
Что такое тг?
телеграм
Facebook.
поможете решить ещё пару задач?)))
Да.
давайте всё обсудим в фейсбуке)))
Хорошо.
https://www.facebook.com/shahzod.sharky
ссылка на мой аккаунт))
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Окружающий мир,
автор: пуля2536
Предмет: Английский язык,
автор: кристя210
Предмет: Українська мова,
автор: Kristikoval12