Задание приложено...
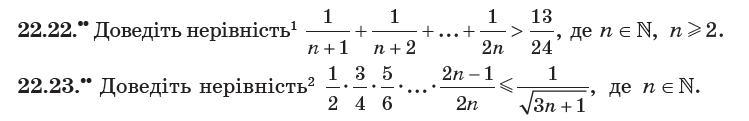
Ответы
Ответ:
Метод математической индукции:
Для того, чтобы доказать, что некоторое утверждение верно при натуральном необходимо выполнить следующие условия:
База индукции:
- 1) Доказать, что утверждение верно при
или при каком либо другом конкретном натуральном
(в этом случае утверждение будет доказно от
и для всех последующих натуральных чисел).
Индуктивный переход:
- 2) Сделать гипотезу, что утверждение верно для
и на основании данной гипотезы доказать, что утверждение верно для
Если выполнены утверждения 1) и 2), то исходное утверждение доказано для всех натуральных методом математической индукции.
22.22
Воспользуемся методом математической индукции:
База индукции:
а)
- верно
Индуктивный переход:
- пусть верно
Необходимо доказать:
Так как по предположению индукции - верно, то при прибавки положительного числа
(так как
) неравенстов также будет выполнятся.
Утверждение для верно, тогда методом математической индукции доказано, что
при
и
.
22.23
Воспользуемся методом математической индукции:
База индукции:
- верно
Индуктивный переход:
- пусть верно
Необходимо доказать:
Так как , то знаменатель дроби всегда больше нуля. Проебразуем числитель:
1)
2)
3)
То есть неравенство выполняется при
Утверждение для верно, тогда методом математической индукции доказано, что
при
.