Question

Задача по геометрии
Высота правильной треугольной пирамиды 6см, а боковая грань состовляет с плоскостью основания угол 30 градусов. Найти S полной поверхности

Answer 1

ОТВЕТ: площадь полной поверхности равна 324(√3+2) см^2

УСЛОВИЕ: Высота правильной треугольной пирамиды 6см, а боковая грань составляет с плоскостью основания угол 30 градусов.

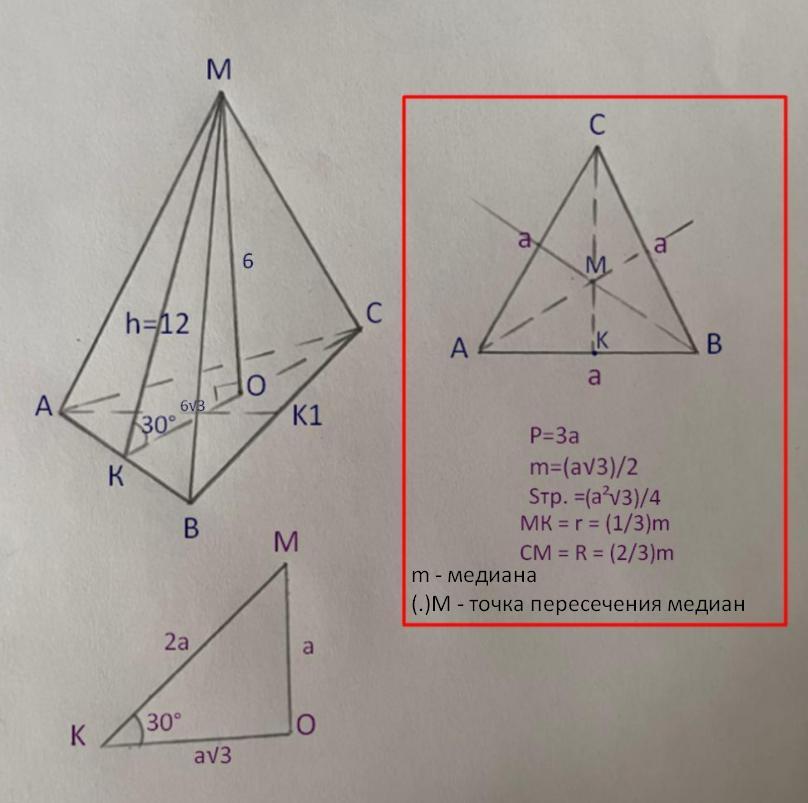
Дано: ОМ = 6см, ∠МКО = 30°

Найти: Sпол. = Sосн. + Sбок.

            Sбок. = (Pосн. * h)/2

            МК = h - апофема

РЕШЕНИЕ:

1) ΔМКО: ∠О=90°, ∠К=30° (т.к ∠МКО - это линейный угол двугранного угла АMB и ABC (две грани), а линейный угол - это угол между двумя перпендикулярами, проведённые из одной точки на ребре (АВ) в каждой грани. СК - медиана, высота, биссектриса, т.к СК ⊥ АВ
Рассмотрим ΔАМВ: МК ⊥ АВ т.к она медиана в равнобедренном треугольнике АМВ, таким образом из (.)К проведены 2 перпендикуляра КС (которой ⊥ АВ) и КМ (который ⊥ АВ).

Затем:

           МО=6см, то КМ=2*6=12см - h апофема, КО=6√3

2) КО = $\large \boldsymbol {}\frac{1}{3} m$

  $\large \boldsymbol {} 6\sqrt{3} =\frac{1}{3} *\frac{a\sqrt{3} }{2}$

  $\large \boldsymbol {} 6\sqrt{3} =\frac{a\sqrt{3} }{6}$ | *6

  $\large \boldsymbol {} 36\sqrt{3} =a\sqrt{3}$ | √3

   $\large \boldsymbol {} a=36$ (см) -  сторона основания

3) Sосн. = $\large \boldsymbol {} \frac{36^2\sqrt{3} }{4} =9*36\sqrt{3} =324\sqrt{3}$ (см²) ;

4) Sбок. = $\large \boldsymbol {}\frac{3*36*12}{2} =18*36=648$  (см²) ;

5) Sпол. = $\large \boldsymbol {} 324\sqrt{3} +648=324(\sqrt{3} +2)$ см²

Удачи!