Question

СРОЧНО ДАЮ 20 БАЛЛОВ!
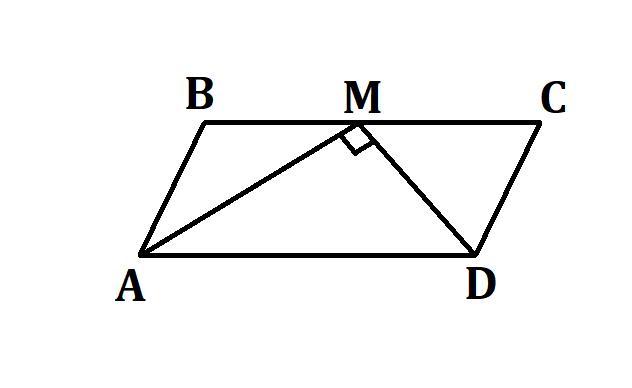
в параллелограмме ABCD биссектриса угла A равного 60° пересекает сторону BC в точке M отрезки AM и DM перпендикулярны. найдите периметр параллелограмма если ab=4

Answer 1

Ответ: периметр параллелограмма равен 24

Пошаговое объяснение:

• Противоположные стороны параллелограмма параллельны и равны.

⇒ BC || AD, по свойству параллелограмма

∠BAD + ∠ABC = 180°, как односторонние при пересечении BC || AD секущей AB.

⇒ ∠ABC = 180° - ∠BAD = 180° - 60° = 120°

Так как AM - биссектриса, по условию ⇒ ∠BAM = ∠MAD = ∠BAD : 2 = 60° : 2 = 30°

Так как AM ⊥ MD, по условию ⇒ ΔAMD - прямоугольный

• Сумма острых углов в прямоугольном треугольнике равна 90°.

⇒ ∠MAD + ∠MDA = 90° ⇒ ∠MDA = 90° - ∠MAD = 90° - 30° = 60°

• Противоположные углы параллелограмма равны.

⇒ ∠ABC = ∠ADC = 120°

∠MDC = ∠ADC - ∠ADM = 120° - 60° = 60°

Так как ∠MDC = ∠ADM = 60° ⇒ MD - биссектриса.

• Биссектриса угла параллелограмма отсекает от параллелограмма равнобедренный треугольник.

Так как AM - биссектриса ⇒ ΔABM - равнобедренный

• В равнобедренном треугольнике боковые стороны равны.

AB = BM = 4, по свойству равнобедренного треугольника

Так как MD - биссектриса ⇒ ΔMCD - равнобедренный.

По свойству параллелограмма, AB = CD

MC = CD = 4, по свойству равнобедренного треугольника.

⇒ BC = BM + MC = 4 + 4 = 8

• Периметр фигуры - сумма длин всех её сторон.

⇒ P = (AB + BC) · 2 = (4 + 8) · 2 = 12 · 2 = 24