Предмет: Алгебра,
автор: yydfhf
Помогите пожалуйста с log
Приложения:
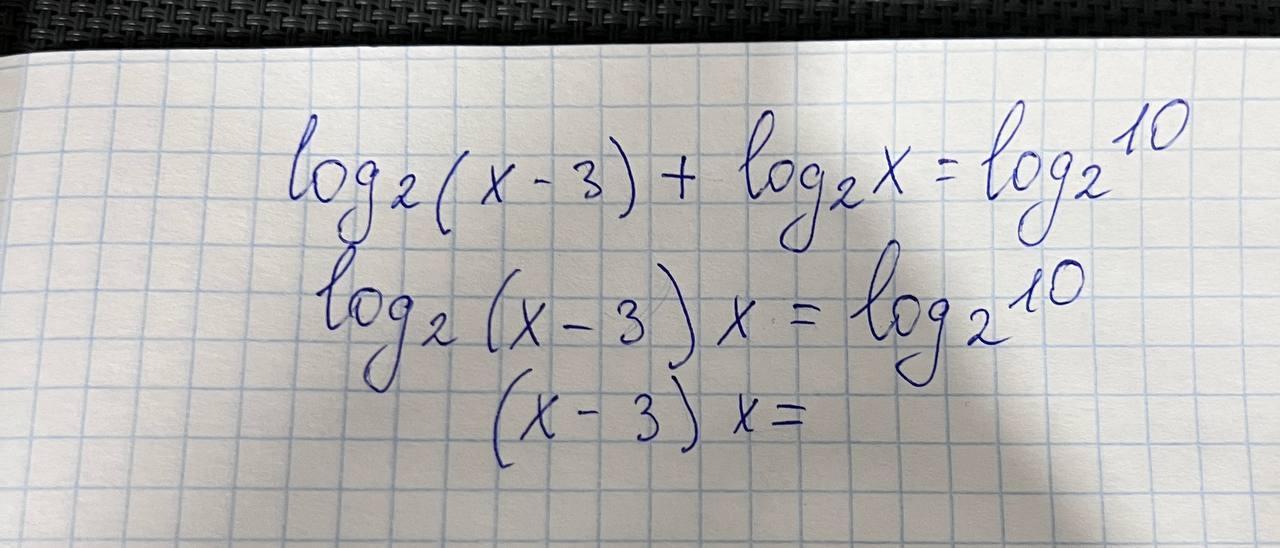
Ответы
Автор ответа:
0
Ответ:
х = 5
Объяснение:
_________________________
ОДЗ:
_________________________
- не подходит по ОДЗ
ddhehdydyfyydyyyeeyt:
здрастуйте, помогите задание мне с матиматикой
Автор ответа:
0
Похожие вопросы
Предмет: Черчение,
автор: олег580
Предмет: Английский язык,
автор: норик16
Предмет: Английский язык,
автор: Кимбасимба
Предмет: Алгебра,
автор: Аноним
Предмет: Английский язык,
автор: annab8