Question

Помогите с высшей математикой пожалуйста

Answer 1

Ответ:

4. Длина дуги данной кривой равна 9,1 ед.

5. Объем тела, образованного вращением вокруг оси Ох равно 0,94 ед.³

Пошаговое объяснение:

Требуется найти длину дуги кривой и вычислить объем тела, образованного вращением вокруг оси Ох.

4. (у + 1)² = х³ от точки пересечения с осью Оу до точки пересечения с прямой у = 7.

Так как левая часть больше или равна 0 ⇒ х ≥ 0

Формула длины кривой:

$\displaystyle \boxed { L = \int\limits^b_a {\sqrt{1+(y')^2} } \, dx }$

Найдем предела интегрирования.

Для этого найдем точки пересечения с осью Оу (х = 0) и с прямой у=7.

1) х = 0

(у + 1)² = 0

у = -1

Получим точку (0; -1)

2) у = 7

(7 + 1)² = х³

64 = х³

х = 4

Получим точку (4; 7)

Следовательно а = 0; b = 4.

Найдем производную, для этого выразим у:

$\displaystyle (y+1)^2=x^3\;\;\;\Rightarrow \;\;\;y=\sqrt{x^3}-1 =x^{\frac{3}{2} }-1$

$\displaystyle y'=\frac{3}{2}x^{\frac{3}{2}-1 } =\frac{3}{2} x^{\frac{1}{2} }$

Найдем длину дуги:

$\displaystyle L=\int\limits^4_0 {} \sqrt{1+\frac{9}{4}x } \;\, dx$

Выполним замену переменной:

$\displaystyle 1 +\frac{9}{4}x=t\\ \\dx=\frac{4}{9}dt$

Заменим пределы интегрирования:

х = 0 ⇒ t = 1

x = 4 ⇒ t = 10

Найдем интеграл:

$\displaystyle \frac{4}{9} \int\limits^{10}_1 {t^{\frac{1}{2} }} \, dx =\frac{4}{9}\cdot\frac{2t^{\frac{3}{2} }}{3}\bigg|^{10}_1 =\frac{8}{27} (\sqrt{10^3} -1)=\frac{8}{27}(10\sqrt{10}-1)\approx 9,1$

Длина дуги данной кривой равна 9,1 ед.

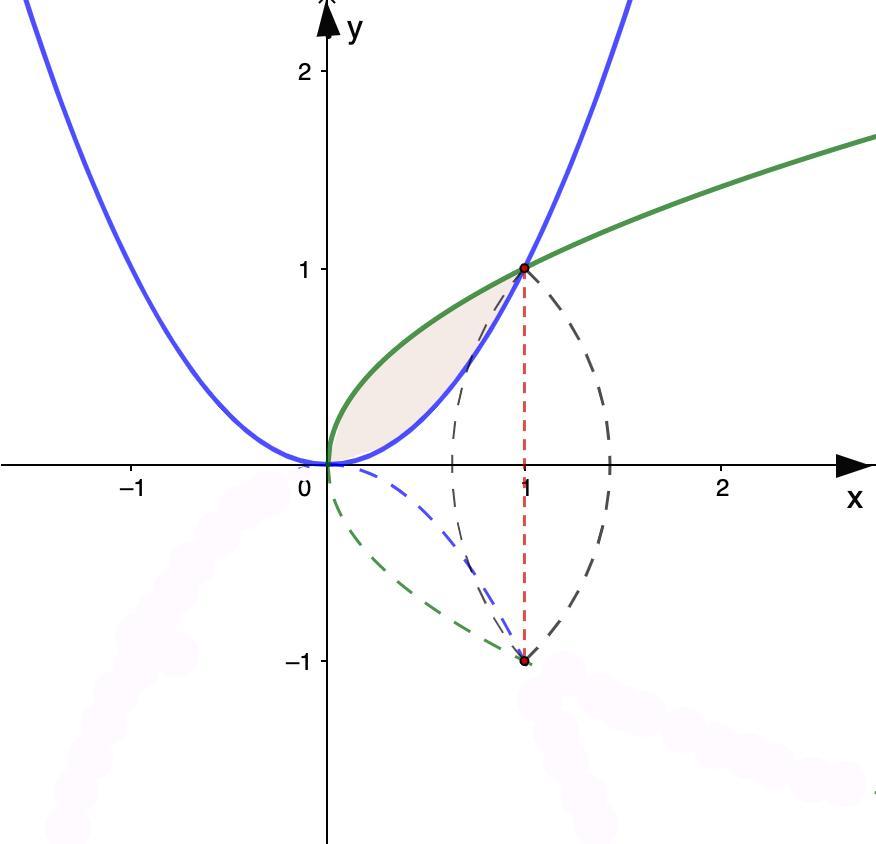
5. у = х²; у = √х

Построим графики функций.

Найдем абсциссы точек пересечения графиков.

х² = √х

х = 0   и   х = 1

b = 1; a = 0.

Объем тела вращения найдем по формуле:

$\displaystyle \boxed { V_x=\pi \int\limits^b_a {f^2(x)} \, dx }$

Объем данного тела равен разности объемов:

$\displaystyle V_x=\pi \int\limits^1_0 {(\sqrt{x} )^2} \, dx -\pi \int\limits^1_0 {(x^2)^2} \, dx =\pi \left(\int\limits^1_0 {x} \, dx -\int\limits^1_0 {x^4} \, dx \right)=\\\\\pi \left(\frac{1}{2}x^2-\frac{1}{5}x^5\right)\bigg| ^1_0=\pi\left (\frac{1}{2}-\frac{1}{5}-0\right) =\frac{3}{10} \pi =0,3\pi\approx 0,94$

Объем тела, образованного вращением вокруг оси Ох равно 0,94 ед.³