Предмет: Алгебра,
автор: leintevaalena23
Помогите с производными
Приложения:
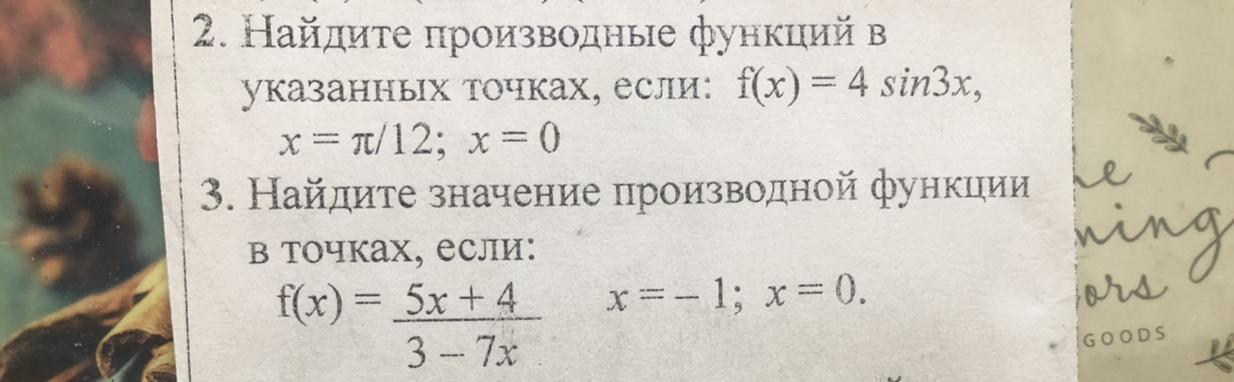
Ответы
Автор ответа:
1
Теория:
Нахождение производной сложной функции:
f(g(x)) = (g(x))' * (f(g(x)) )'
Нахождение производной дроби:
Решение:
2)
3)
Автор ответа:
1
Ответ:
во вложении
Объяснение:
там же
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: оля1375
Предмет: Русский язык,
автор: ir4ik7
Предмет: Английский язык,
автор: svetilnyk
Предмет: Обществознание,
автор: daria0239
Предмет: Русский язык,
автор: kaput06