Question

Точки А, В и С сферы лежат на поверхности так, что АВ = ВС = = 12 см, <BAC = 30°. Найдите площадь поверхности сферы, если известно, что расстояние от центра сферы до плоскости тре угольника АВС равно 3 см. ​

Answer 1

Ответ:

612π см²

Объяснение:

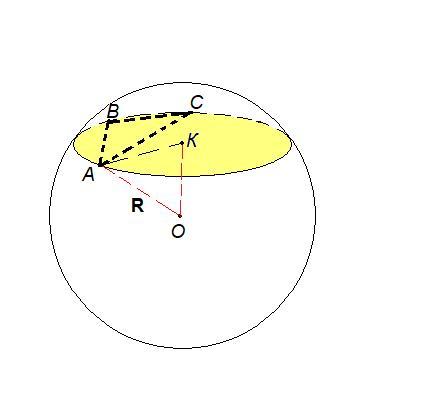
Треугольник АВС вписан в сечение сферы - в окружность с центром К.

• Отрезок, соединяющий центр сферы с центром сечения, перпендикулярен плоскости сечения.

ОК ⊥ (АВС), значит ОК = 3 см - расстояние от центра сферы до плоскости.

• По следствию из теоремы синусов, отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу описанной окружности:

$\dfrac{BC}{\sin\angle BAC}=2\cdot KA$

$\dfrac{12}{\frac{1}{2}}=2KA$

KA = 12 см

ΔАКО:  ∠АКО = 90°, по теореме Пифагора

 R = AO = √(KA² + OK²) = √(12² + 3²) = √(144 + 9) = √153 = 3√17 см

Площадь поверхности сферы:

S = 4πR²

S = 4 · π · (3√17)² = 4 · π · 9 · 17 = 612π см²