Предмет: Алгебра,
автор: danya111839
помогите вычислить значение производной!! заранее спасибо!
Приложения:
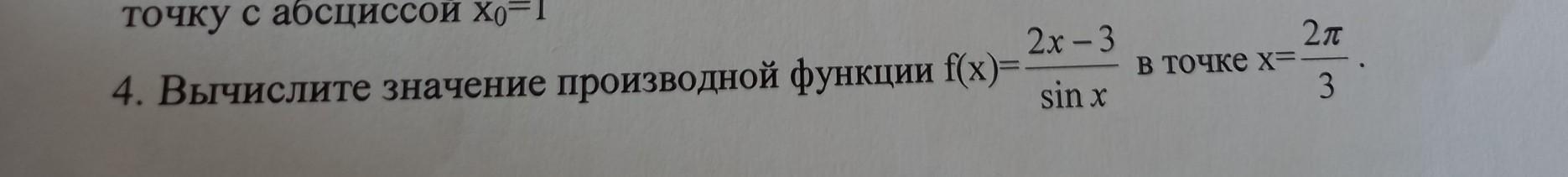
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: mila237
Предмет: Русский язык,
автор: elin497
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: ludazo2007
Предмет: Математика,
автор: SHPION0AGENT