Question

Дана функция f(x)=1/3x^3-4x^2+15x-7. a) найдите критические точки функции b) определите промежутки многотонности c) запишите уравнение касательной функции при x0=1 d) найдите область определения и используя результаты пунктов a) и d) постройте схематически график функции

Answer 1

Ответ:

а)  критические точки:    x₁ = 5  (точка локального минимума);

                                           x₂ = 3 (точка локального максимума).

b) интервалы монотонности :

(-∞ ;3) функция возрастает;

(3; 5)  функция убывает;

(5; +∞)     функция возрастает.

с) уравнение касательной:       $\displaystyle \boldsymbol {y_k=8x- \frac{11}{3}}$

d) ООФ ;  x ∈ R

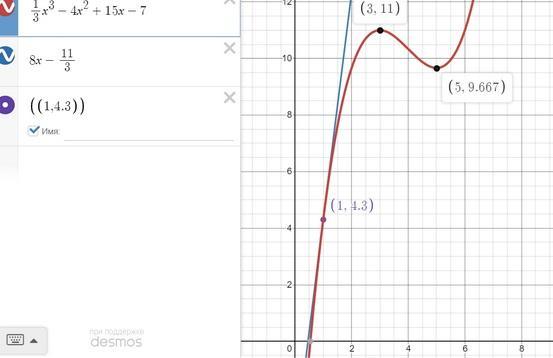
График на рисунке

Пошаговое объяснение:

Для всех пунктов нам понадобится первая производная.

Найдем ее.

$\displaystyle f'(x) = \bigg (\frac{1}{3} x^3-4x^2+15x-7\bigg)'= \bigg (\frac{1}{3} x^3\bigg)'-(4x^2)'+(15x)'-(7)'=\\\\\\=\frac{1}{3} *3x^2-4*2x+15*1-0=\boldsymbol {\underline {x^2-8x+15}}$

Ну и теперь пошли по пунктам.

a) найдите критические точки функции

• Критические точки функции - это точки, в которых  производная функции равна нулю или не существует.

Наша производная существует везде, поэтому найдем точки, в которых она равна 0

х² -8х +15 = 0;   ⇒    x₁ = 5;    x₂ = 3 - это критические точки;

Какая из этих точек локальный минимум, а какая локальный максимум, можно определить и в пункте b), но у нас есть ссылка именно на пункт а), поэтому найдем локальные  минимум и максимум здесь.

Используем достаточное условие экстремума функции.

Найдем вторую производную:

f''(x) = 2x-8

• Если в точке х₀  f''(x₀) < 0, то точка x₀ - точка  локального/глобального  максимума.

• Если в точке х₀  f''(x₀) > 0, то точка x₀ - точка локального/глобального минимума.

f''(5) = 2 > 0 - значит точка x₀ = 5 точка локального минимума

                                                       функции.

y''(3) = -2 < 0 - значит точка x₀ = 3 точка локального максимума

                                                       функции

Значение функции в точках локального  минимума и максимума (для построения графика)

$\displaystyle \boldsymbol { f(5) = \frac{29}{3} =9\frac{2}{3} \qquad f_{min}}$

$\displaystyle \boldsymbol { f(3) = 11\qquad \qquad \quad f_{max}}$

b) определите промежутки монотонности

Используя данные пункта а), а именно критические точки,  разбиваем область определения функции на интервалы и смотрим, где производная (не функция!)  больше нуля, а где меньше.

(-∞ ;3) f'(0) = 15 > 0, значит функция возрастает;

(3; 5) f'(4) = (-1) < 0, значит функция убывает;

(5; +∞)      f'(6) = 3 > 0  значит функция возрастает.

Вот здесь можно также определить локальные минимум и максимум (это второй способ).

В окрестности точки x₀=3 производная функции меняет знак с "+" на "-", значит точка x₀=3  - точка  локального максимума.

В окрестности точки x₀=5 производная функции меняет знак с "-" на "+", значит, точка x₀=5 - точка  локального минимума.

c) запишите уравнение касательной функции при x₀=1

Уравнение касательной в точке х₀ имеет вид

$\displaystyle y_k = f(x_0) + f'(x_0)(x - x_0)$

Найдем нужные значения

$\displaystyle f(1) = \frac{13}{3}$

$f'(1) = 8$

Теперь мы легко напишем уравнение касательной

$\displaystyle \boldsymbol {\underline {y_k=\frac{13}{3} +8(x-1) }}$

и преобразуем ее к привычному иду

$\displaystyle \boldsymbol {\underline {y_k=8x- \frac{11}{3} }}$

d) найдите область определения и используя результаты пунктов a) и d) постройте схематически график функции

область определения функции    вся числовая ось  x ∈ R.

Теперь график.

Я, к сожалению, плохо рисую от руки, поэтому я построю график точный, а Вы уже от руки перерисуете.

И не пугайтесь десятичных дробей на графике. Все значения в обычных дробях есть в тексте.