Предмет: Алгебра,
автор: skoropad2006
ДАЮ 30 БАЛЛОВ !!!
ПОМОГИТЕ ПЛЗ
Приложения:
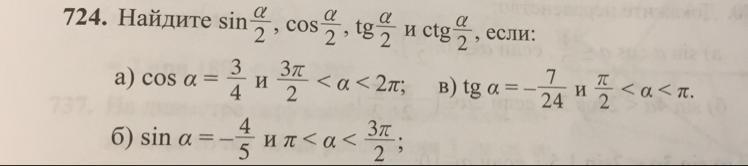
Ответы
Автор ответа:
1
Ответ:
а)
б)
в)
Объяснение:
а)
Дано:
Найти:
Решение
т.е. имеем, что находится в IV четверти координатной плоскости; тогда как
- во II четверти, а следовательно:
Т.к. нам известно значение целого угла, cos α, через него можно выразить тригонометрические функции половинного угла.
Выразим и найдем значение для и
Используя то, что тангенс угла равен отношению синуса этого угла к косинусу, а котангенс - отношению косинуса этого угла к синусу, получаем:
Соберем воедино и получим
Ответ:
б), в)
см. приложенные файлы
Приложения:


skoropad2006:
ОГРОМНОЕ СПАСИБО
Похожие вопросы
Предмет: Қазақ тiлi,
автор: soiifia
Предмет: Русский язык,
автор: ainurzhaksybayeva
Предмет: Русский язык,
автор: шилохвостова1
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: солнышко345