Предмет: Алгебра,
автор: eleonaise
Демо задание 1-3
Номер 4
Приложения:
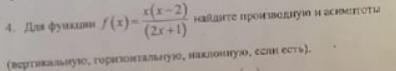
Ответы
Автор ответа:
3
Ответ:
b) Вертикальная асимптота х=а, если .
Проверим точку а= -0,5 , так как при х= -0,5 функция не существует, знаменатель дроби обращается в ноль .
Вертикальная асимптота х= -0,5 .
c) Наклонная асимптота y=kx+b .
Уравнение наклонной асимптоты или
.
Горизонтальной асимптоты нет .
Похожие вопросы
Предмет: Русский язык,
автор: александра415
Предмет: Русский язык,
автор: АняКонник16
Предмет: Русский язык,
автор: диас110
Предмет: Математика,
автор: Dhara
Предмет: Геометрия,
автор: ТвояМарго