Question

На полу ангара для работы клуба робототехников намечены две точки - Үи С. Два робота выехали навстречу друг другу из этих точек, двигаясь по прямой с постоянной скоростью. Встретились они за 7 м от Y, оба после встречи прошли весь путь до конца, развернулись и снова встретились, теперь уже за 9 м от С. Какова была длина всего пути между точками Y и С?

Помогите пожалуйста дам 40 баллов
как можно скорее помогите ​

Answer 1

Ответ:

12 м

Объяснение:

Обозначим расстояние YC = S, а скорости роботов v1 и v2.

Один робот выехал из Y и проехал 7 м.

Второй робот выехал из С и проехал S-7 м за то же время:

7/v1 = (S-7)/v2

Дальше они поехали до конца, потом развернулись и поехали опять навстречу друг другу.

Первый робот проехал S+9 м, а второй робот 2S-9 м за то же время.

(S+9)/v1 = (2S-9)/v2

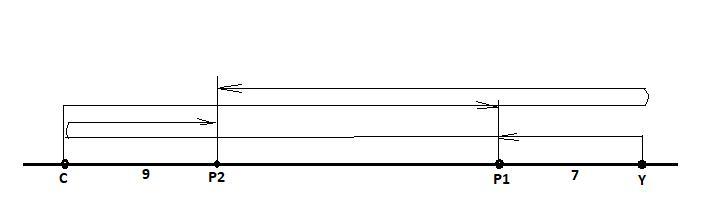
Весь их путь я изобразил на рисунке.

По правилу пропорций получаем систему:

{ 7*v2 = (S-7)*v1

{ (S+9)*v2 = (2S-9)*v1

Раскрываем скобки:

{ 7*v2 = S*v1 - 7*v1

{ S*v2 + 9*v2 = 2S*v1 - 9*v1

Выделим S:

{ S*v1 = 7(v1 + v2)

{ S(2v1 - v2) = 9(v1 + v2)

Подставим v1 + v2 из 1 уравнения во 2 уравнение:

{ v1 + v2 = S*v1/7

{ S(2v1 - v2) = 9*S*v1/7

Сокращаем S:

2v1 - v2 = 9v1/7

v2 = 2v1 - (9/7)v1 = 5/7*v1

Подставляем в 1 уравнение:

v1 + v2 = v1 + 5/7*v1 = 12/7*v1 = S*v1/7

Сокращаем v1:

12/7 = S/7

S = 12 м