Предмет: Алгебра,
автор: danaaitzhanova
вычислите площадь фигуры, ограниченной линиями (ответ округлите до единиц) :
у = 2^х, у=2^-х, у =2
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Вычислить площадь фигуры, ограниченной линиями:
y = 2^x; y = 2^(-x); y = 2
Решение:
Найдём точки пересечения этих графиков:
1) 2^x = 2^(-x)
x = -x
x = 0; y(0) = 2^0 = 1
2) 2^x = 2
x = 1; y = 2
3) 2^(-x) = 2
x = -1; y = 2
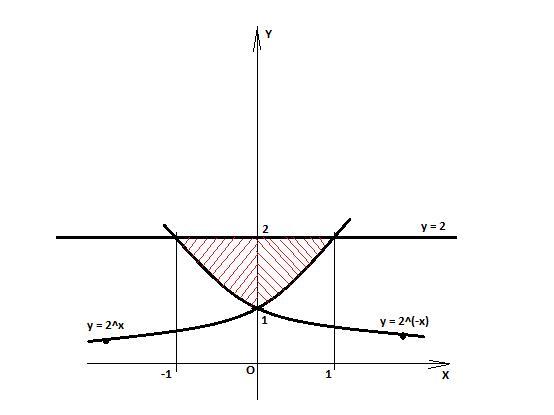
Графики представлены на рисунке.
Две половины нужной площади выделены разной штриховкой.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: ралл2
Предмет: Українська мова,
автор: Аноним
Предмет: Русский язык,
автор: daryasamorai
Предмет: Математика,
автор: 1MissK1982
Предмет: Русский язык,
автор: nigarelihesenova