Question

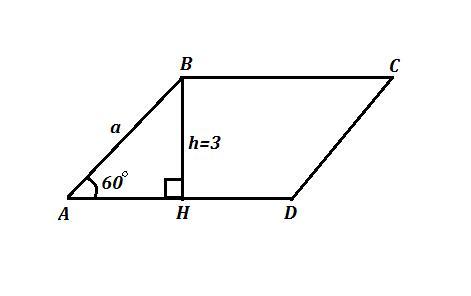
249. Вычислите площадь ромба, высота которого равна 3, а острый угол в 2 раза меньше тупого.​

Answer 1

Ответ:

P=4a = 4*2=8

Объяснение:

острый угол = 180- тупой угол

H=√3 . пусть х острый угол , тогда тупой 2x ,

3x=180

x=60 гр , значит углы равны 60 и 120 градусов

Опустим высота получим прямоугольный треугольник

√3/sin60=a где "а" сторона ромба

a=2

P=4a = 4*2=8

Answer 2

Ответ:

Высота ромба равна h=BH=3 ,  h ⊥ a  или  BH⊥AD .

Обозначим сторону ромба через  а , острый угол - через  х° .

Тогда тупой угол равен 2х° . Так как сумма углов, прилежащих к одной и той же стороне ромба, равна 180°, то  х°+2х°=180° , 3х°=180° ,

х°=60°  - острый угол

Рассмотрим  ΔАВН , ∠АНВ=90° ,  а=h/sinx° ,

АВ=BH/sin60°=3/(√3/2)=2√3 .

Площадь ромба равна  $S=ah=2\sqrt3\cdot 3=6\sqrt3$  .

Или   $S=a^2\cdot sin60^\circ =(2\sqrt3)^2\cdot \dfrac{\sqrt3}{2}=12\cdot\dfrac{\sqrt3}{2}=6\sqrt3$  .