Предмет: Алгебра,
автор: olli45
Найдите пожалуйста f’(x)!!! Задание на фото.
(50 баллов)
...
Приложения:
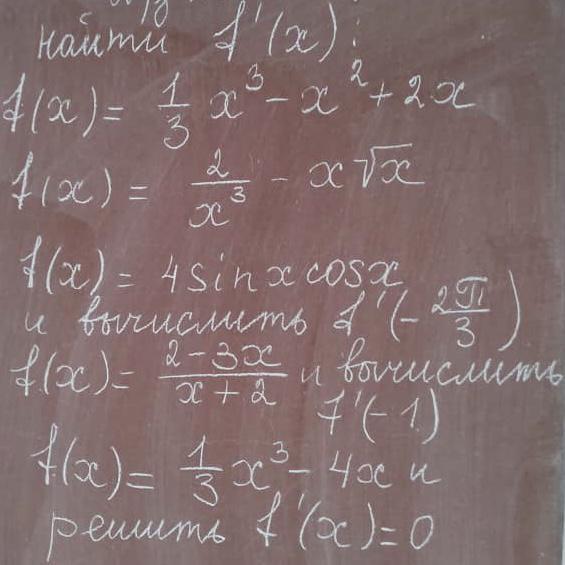
Ответы
Автор ответа:
3
Ответ.
Аноним:
ваш ответ сбился!
сами посмотрите (
у меня всё нормально ... претензии не ко мне, а к программистам...
Спасибо большое!
Похожие вопросы
Предмет: Русский язык,
автор: Лейла559
Предмет: Русский язык,
автор: Masha2281337
Предмет: Другие предметы,
автор: lolitkapipitka
Предмет: Математика,
автор: kooko81
Предмет: Алгебра,
автор: ochko42