Предмет: Алгебра,
автор: FaerVator
помогите пожалуйста ))
Приложения:
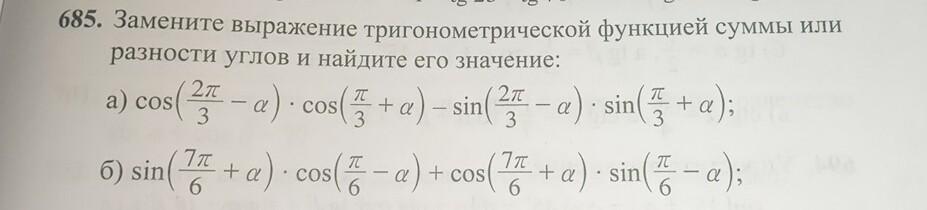
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: Иван811
Предмет: Английский язык,
автор: 6occ9lpa228
Предмет: Другие предметы,
автор: Маломака
Предмет: Астрономия,
автор: Emeluanew
Предмет: Математика,
автор: igor12388