Question

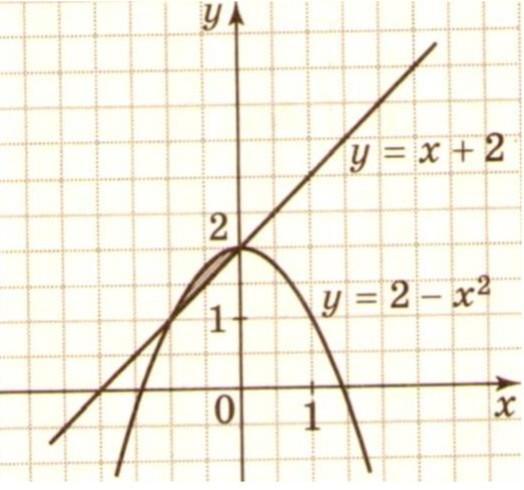
Знайдіть за малюнком площу заштрихованої фігури.​

Answer 1

Ответ:

$S = \dfrac{1}{6} .$

Пошаговое объяснение:

Точки пересечения графика прямой и графика параболы имеют координаты

х₁ = -1;  и  х₂ = 0

Заштрихованная площадь определяется через интеграл

$S = \int\limits^{x_2}_{x_1} {(f_2(x) -f_1(x)) } \, dx$

здесь

f₁(x) = 2 - x²       f₂(x) = x + 2

Тогда заштрихованная площадь

$S = \int\limits^{0}_{-1} {((2 - x^2) -(x + 2) )} \, dx = \int\limits^{0}_{-1} {( - x^2 -x )} \, dx =\\ \\ =\Big (-\dfrac{x^3}{3}- \dfrac{x^2}{2}\Big )\Bigg |^0_{-1} =0-\Big (-\dfrac{(-1)^3}{3}- \dfrac{(-1)^2}{2}\Big ) =\\ \\= -\dfrac{1}{3} + \dfrac{1}{2} = \dfrac{3}{6} - \dfrac{2}{6} = \dfrac{1}{6} .$