Дана симметричная игральная кость - при каждом броске выпадение любого числа очков от 1 до 6 равновероятно. Эту кость бросили три раза. Известно, что в сумме выпало 7 очков. Какова вероятность того, что ни при одном из бросков не выпало 4 очков?
Ответы
Ответ:
60%
Объяснение:
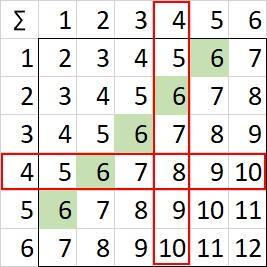
В приложении показана таблица сумм очков после двойного бросания кубика. Если третий раз выпало 1 очко, то два предыдущих дали в сумме 6. Эти значения в таблице выделены зеленым цветом. Всего их 5, а два из них содержат вариант, когда выпало 4 очка (красным выделен столбец и строка).
Т.е. 1+6: 5 вариантов всего, 2 с 4кой.
Рассмотрим вариант, когда третьим бросанием выпало 2 очка, тогда предыдущая сумма равна 5 и таких значений в таблице 4 и два из них с использованием 4ки.
2+5: 4 варианта всего, 2 с 4кой
Рассматриваем следующие варианты:
3+4: 3 варианта всего, ни одного с 4кой
4+3: 2 варианта всего, оба с 4кой, потому что третье бросание 4
5+2: 1 вариант, ни одного с 4кой
6+1: быть не может.
Таким образом всего 15 варинтов, когда в сумме выпадет 7 очков, и все они равновероятны, из них 9 варинатов, когда среди выпавших значений нет 4ки.
Вероятность того, что ни при одном из бросков не выпало 4 очков:
P = 9/15 = 3/5 = 0.6 = 60%