Question

ДАЮ 35 БАЛЛОВ!!! Найти площадь криволинейной трапеции при помощи первообразной + построить графики самих функций (смотреть прикрепленное фото)

Answer 1

Ответ:

1. Площадь фигуры, ограниченной линиями y = (x - 1)²+3,   y = 0,   x = 0,   x=3, равна 12 ед².

2. Площадь фигуры, ограниченной линиями у = -х² +4, у = -х - 2, равна $\displaystyle 20\frac{5}{6}$  ед².

Пошаговое объяснение:

Требуется найти площадь криволинейной трапеции при помощи первообразной и построить графики самих функций.

Площадь криволинейной трапеции найдем по формуле:

$\displaystyle \boxed {S=\int\limits^b_a {(f_1(x)-f_2(x))} \, dx }$

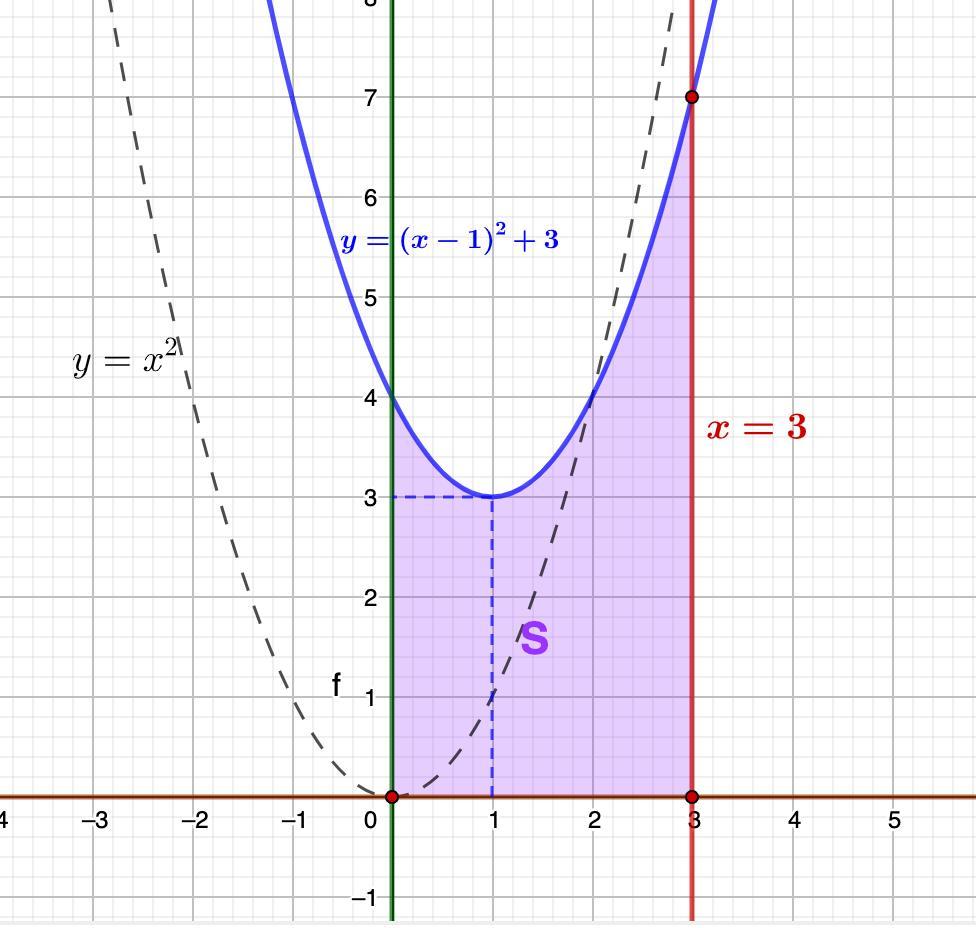
1. y = (x - 1)²+3,   y = 0,   x = 0,   x=3.

Построим данные графики и определим искомую площадь.

1) у = (х - 1)² + 3

-парабола, ветви вверх.

Построим классическую параболу у = х².

График у = (х - 1)² + 3 получается из графика у = х² путем сдвига на одну единицу вправо и на три единицы вверх.

2) Рассмотрим остальные графики:

у = 0 - это ось 0х;

х = 0 - это ось 0у;

х = 3 - прямая, параллельная оси 0у.

3) Получили площадь (см. рисунок):

f₁(x) =  (х - 1)² + 3;

f₂(x) = 0

b = 3; a = 0.

Подставим эти значения в формулу и найдем площадь:

$\displaystyle S=\int\limits^3_0 {((x-1)^2+3)-0)} \, dx =\int\limits^3_0 {(x^2-2x+4)} \, dx=\\\\=\left(\frac{x^3}{3}-2\cdot \frac{x^2}{2}+4x\right)\bigg| ^3_0= \left(\frac{x^3}{3}-x^2+4x\right)\bigg| ^3_0=\\\\=\frac{3^3}{3}-3^2+4\cdot 3=9-9+12=12$

Площадь фигуры, ограниченной линиями y = (x - 1)²+3,   y = 0,   x = 0,   x=3, равна 12 ед².

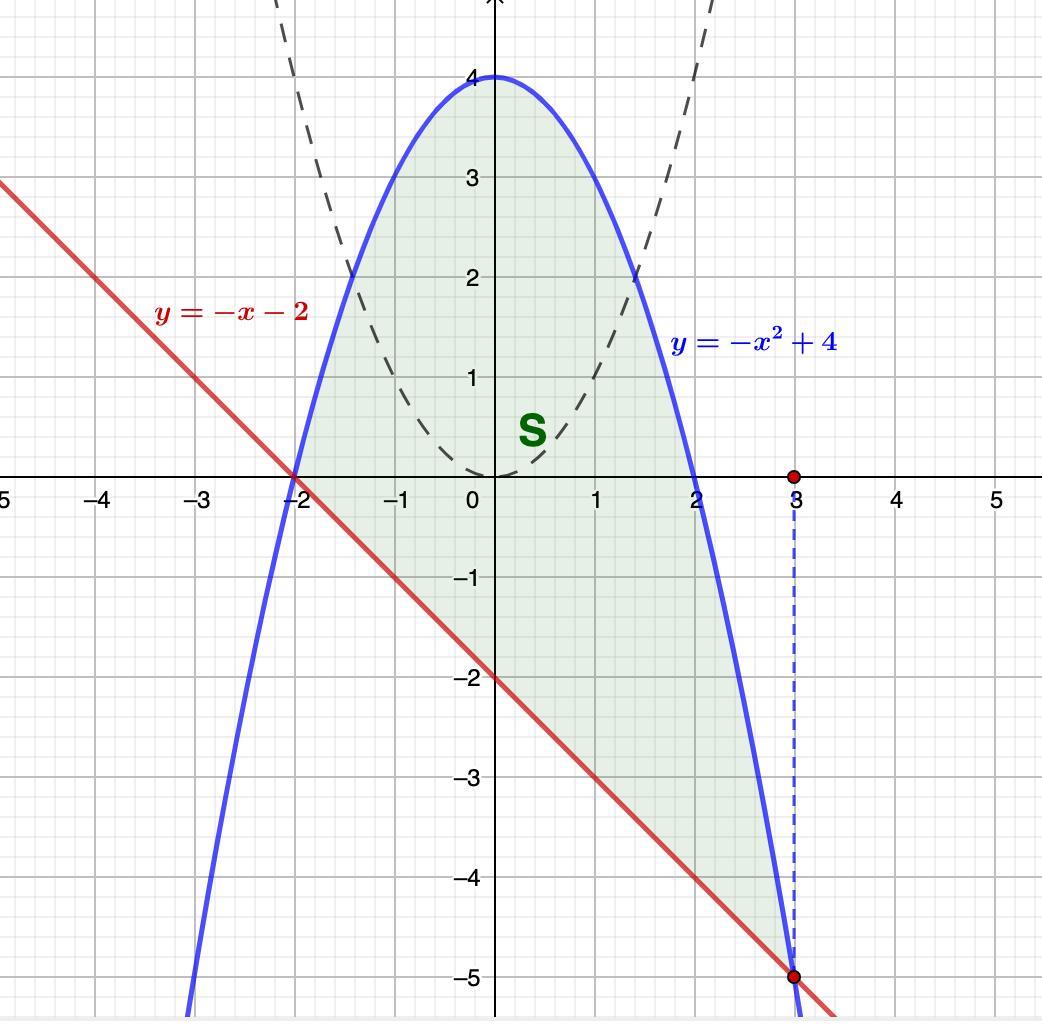
2. у = -х² +4, у = -х - 2

Построим данные графики и определим искомую площадь.

1)   у = -х² +4

- парабола, ветви вниз.

Данный график получается из параболы у = х² путем зеркального отображения относительно оси 0х и сдвигом на четыре единицы вверх.

2) у = -х - 2

- линейная функция, график прямая.

Для построения достаточно двух точек.

х = -2; у = 0

х = 3; у = -5.

3) Найдем точки пересечения этих графиков:

-х² + 4 = -х - 2

х² - х - 6 = 0

По теореме Виета:

х₁ = -2;     х₂ = 3

4) Найдем площадь.

f₁(x) = -x² + 4;

f₂(x) = -x - 2

b = 3; a = -2

$\displaystyle S=\int\limits^3_{-2} {(-x^2+4+x+2)} \, dx =\int\limits^3_{-2} {(-x^2+x+6)} \, dx =\\\\=\left(-\frac{x^3}{3}+\frac{x^2}{2}+6x\right)\bigg|^3_{-2} =\\\\=\left(-\frac{3^3}{3} +\frac{3^2}{2}+6\cdot 3\right)-\left(-\frac{(-2)^3}{3} +\frac{(-2)^2}{2} +6\cdot (-2)\right)=\\\\-9+\frac{9}{2}+18-\frac{8}{3}-2+12 =19+\frac{27}{6}-\frac{16}{6}=19\frac{11}{6}=20\frac{5}{6}$

Площадь фигуры, ограниченной линиями у = -х² +4, у = -х - 2, равна $\displaystyle 20\frac{5}{6}$  ед².

* Использовали формулы:

$\displaystyle \boxed { \int\limits \, dx =x+C}\;;\;\;\;\;\;\boxed {\int\limits {x^a \, dx }=\frac{x^{a+1}}{a+1}+C,\;a\neq -1}$