Question

В прямоугольном треугольнике с катетами 9 и 12 см из вершины прямого угла провели прямую, перпендикулярную гипотенузе данного треугольника. Найди площади получившихся треугольников, включая данный в условии.

В ответе записать площади треугольников через точку с запятой в порядке возрастания в виде натуральных чисел или десятичных дробей

Answer 1

В прямоугольном треугольнике с катетами 9 и 12 см из вершины прямого угла провели прямую, перпендикулярную гипотенузе данного треугольника. Найди площади получившихся треугольников, включая данный в условии.

Ответ:

19,44 см²; 34,56 см²; 54см².

Объяснение:

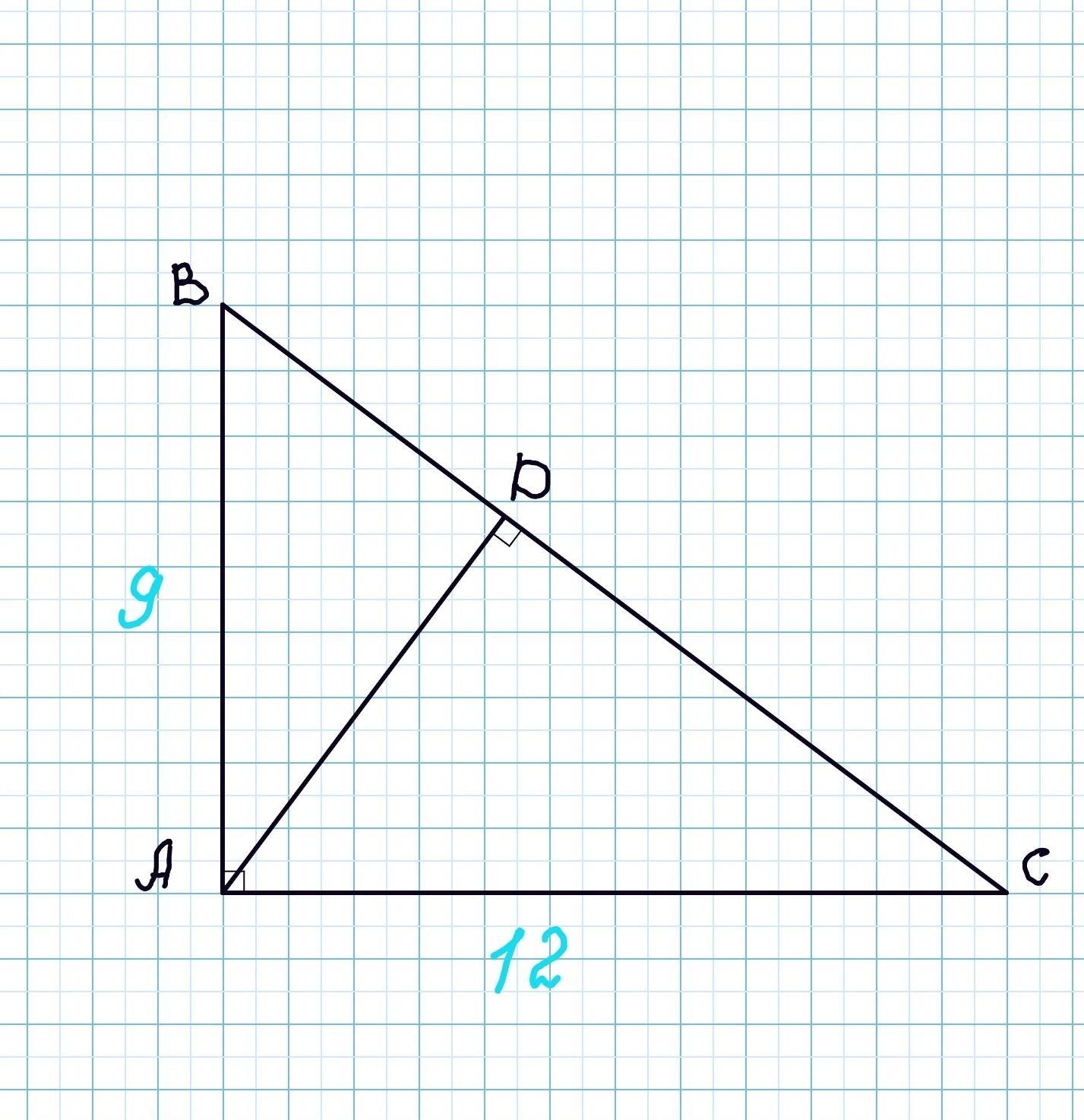
Дано: △АВС - прямоугольный, ∠А=90°, АВ=9см, АС=12 см. AD⟂BC.

Найти: S(ABC), S(ABD), S(ACD).

• Площадь прямоугольного треугольника равна половине произведения его катетов.

S(ABC)=½•AB•AC=½•9•12=54 (см²)

Площадь △ABС равна 54 см²

Найдём гипотезу ВС по теореме Пифагора:

$BC = \sqrt{ {AB}^{2} + {AC}^{2} } = \sqrt{ {9}^{2} + {12}^{2} } = \sqrt{81 + 144} = \sqrt{225} = 15$

BC=15 (см)

• Высота в прямоугольном треугольнике, проведённая к гипотенузе, делит его на два подобных прямоугольных треугольника которые также подобные исходному.

1. △ABD подобен △CBA по двум углам (первый признак подобия):

∠ADB=∠BAC=90°, ∠ABD=∠ABC - как общий.

Найдём коэффициент подобия.

• Коэффициент подобия равен отношению длин соответствующих сторон:

$k_1 = \dfrac{AB}{BC} = \dfrac{9}{15} = \dfrac{3}{5}$

• Отношение площадей подобных треугольников равно квадрату коэффициента подобия:

$\dfrac{S(ABD)}{S(ABC)} = {k_1}^{2} \\ \\ S(ABD) = S(ABC) \times {k_1}^{2} = 54 \times { (\frac{3}{5}) }^{2} = 54 \times \frac{9}{25} = 19,44$

Площадь △ABD равна 19,44 см²

2.△ACD подобен △BCA по двум углам (первый признак подобия):

∠ADC=∠BAC=90°, ∠ACD=∠BCA - как общий.

Найдём коэффициент подобия:

$k _2 = \dfrac{AC}{BC} = \dfrac{12}{15} = \dfrac{4}{5}$

Найдём площадь △ACD:

$\dfrac{S(ACD)}{S(ABC)} = k_2 \\ \\ S(ACD) = S(ABC) \times {k_2}^{2} = 54 \times {( \frac{4}{5}) }^{2} = 54 \times \dfrac{16}{25} = 34,56$

Площадь △ABD равна 34,56 см²