Предмет: Геометрия,
автор: ученица11класса
Найдите объем конуса, если радиус его основания равен 6 дм, а радиус вписанной в конус сферы равен 3 дм
Ответы
Автор ответа:
0
Формула объёма конуса
V=S•h/3
S=πR²=π6²=36π см²
Высоту h=ВН нужно найти.
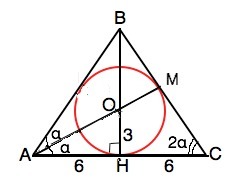
Рассмотрим рисунок осевого сечения конуса с вписанной в него сферой. Это равнобедренный треугольник АВС с вписанной в него окружностью.
АН=6 - радиус основания конуса, О- центр окружности.
ОН=3 - радиус сферы.
BH=AH•tgBAH=6tgBAH
Центр О вписанной в треугольник окружности лежит в точке пересечения биссектрис. ⇒
ВН и АМ - биссектрисы.
Примем угол ОАН=ОАВ=α, тогда угол ВАН=2α
tgα=3/6=0,5
tg2α=2tgα:(1-tg²α)
tg2α=2•0,5:(1-0,5²)=1/0,75⇒
BH=6•(1/0,75)=8 см
V=36π•8:3=96π см³
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: liza553341
Предмет: Русский язык,
автор: temirzhanovnaaselkha
Предмет: Другие предметы,
автор: vasilevadashenka
Предмет: Математика,
автор: привет123409