Предмет: Математика,
автор: Kokse
Пользуясь формулами и правилами дифференцирования, найдите производные функций:
уравнение небольшое
Приложения:
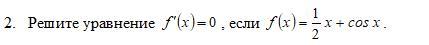
Ответы
Автор ответа:
1
Необходимо знать:
1)
2)
3)
Найдем производную функции :
Решим уравнение :
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: marina277
Предмет: Русский язык,
автор: Нармина23
Предмет: Немецкий язык,
автор: Viktoria00099
Предмет: Обществознание,
автор: floolia