Предмет: Алгебра,
автор: russkihmariya05
УМОЛЯЮ, ПОМОГИТЕ РАЗОБРАТЬСЯ! ДАМ МАКСИМУМ БАЛЛОВ!!!
Меня интересуют номера 3 и 5, как там так получилось? И да, свойства арифметического корня n-й степени я знаю, но даже 5 номер противоречит условию, что "n, m >= 2"
Приложения:
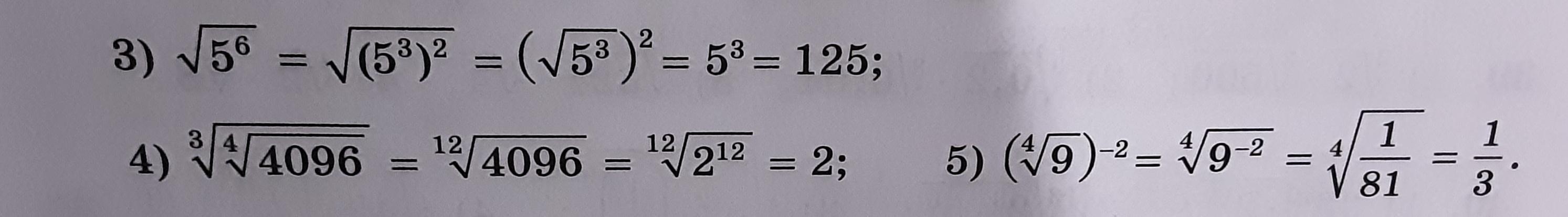
bertramjeratire:
В 3 конкретно что непонятно?
В 3 непонятно, куда потом делась вторая степень, которая была за скобкой
Ответы
Автор ответа:
1
Ответ:
Этот момент можно записать все как
потому что корень это 1/2 степень.
Двойки в степени сокращаются и остаются
5) в 5 как я понял вы не поняли как степень за корнем вошел в него
Запишем оба выражения в виде степени
За скобкой -2 зайдет в скобку с умножением.
А тут уже можно сократить 2 и 4 на два
Если в степени минус, то надо перевернуть число и удалить минус
Степень 1/2 – это корень
Похожие вопросы
Предмет: Русский язык,
автор: марина1062
Предмет: Русский язык,
автор: гуф16
Предмет: Русский язык,
автор: alpenova35
Предмет: Математика,
автор: cjckgxjc