Предмет: Геометрия,
автор: olenamelnn
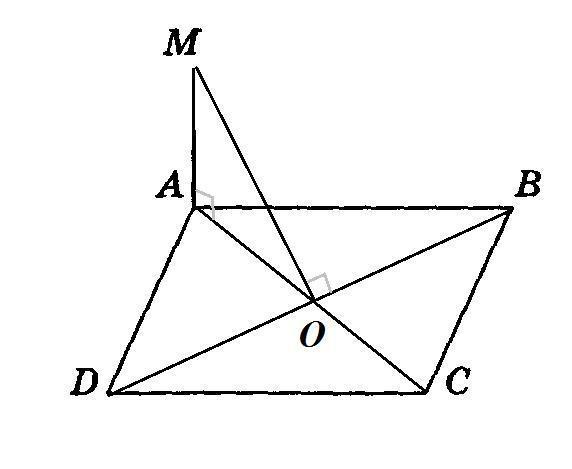
MA — перпендикуляр до площини паралелограма ABCD, O — середина BD і MO ⊥ BD.
1) Визначте вид паралелограма ABCD.
2) Знайдіть відстань від точки M до площини паралелограма, якщо ∠ADC = 60°, AD = 24 см, MA = 13 см.
Ответы
Автор ответа:
3
MO⊥BD
По теореме о трёх перпендикулярах
АО⊥ BD ⇒ диагонали параллелограмма взаимно перпендикулярны, значит АВСD - ромб.
∠АВС=60° ⇒Δ АВС - равносторонний
АС=АВ=ВС=AD=24 cм
АО=(1/2)АС=12 см
По теореме Пифагора из прямоугольного треугольника МАО ( MA⊥ пл. АВСD, значит и прямой АО)
Дано МО=13
Найти МА
МA²=MO²-AO²=13²-12²=169-144=25
MA=5
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: suxarkovs
Предмет: Русский язык,
автор: Дудие
Предмет: Английский язык,
автор: аня1872
Предмет: Қазақ тiлi,
автор: liliana79
Предмет: Физика,
автор: ostapbender007