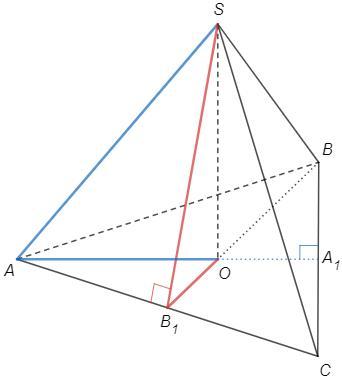
Дан правильный тетраэдр SABC . Выполните рисунок. Найдите: а) синус угла между прямой SA и плоскостью ABC . b) синус угла между плоскостями SAC и ABC . Известно, что длина ребра 6 см.
Ответы
Правильный тетраэдр
- все грани - равносторонние треугольники
- вершина проецируется в центр основания
Центр вписанной и описанной окружностей правильного треугольника - пересечение биссектрис/высот/медиан
a)
Угол между прямой и плоскостью - угол между прямой и ее проекцией.
SO⊥(ABC)
SAO - угол между прямой SA и плоскостью ABC
Все правильные тетраэдры подобны, поэтому примем все ребра =1.
AA1 =AC sin60 =√3/2
Медианы делятся 2:1 от вершины.
AO=2/3 AA1 =2/3 *√3/2 =1/√3
cos(SAO) =AO/SA =1/√3
sin(SAO) =√(1-cos(SAO)^2) =√(1 -1/3) =√(2/3) =√6/3
b)
Угол между плоскостями - угол между перпендикулярами к общей прямой.
SO⊥(ABC), OB1⊥AC => SB1⊥AC (т о трех перпендикулярах)
SB1O - угол между плоскостями SAC и ABC
OB1=1/3 BB1 =1/3 *√3/2 =1/2√3
SB1=√3/2
cos(SB1O) =OB1/SB1 =1/2√3 :√3/2 =1/3
sin(SB1O) =√(1 -1/9) =√(8/9) =2√2/3