Предмет: Алгебра,
автор: samo04
Решите уравнение:

Ответы
Автор ответа:
0
Ответ:
7/4
.........................
Приложения:
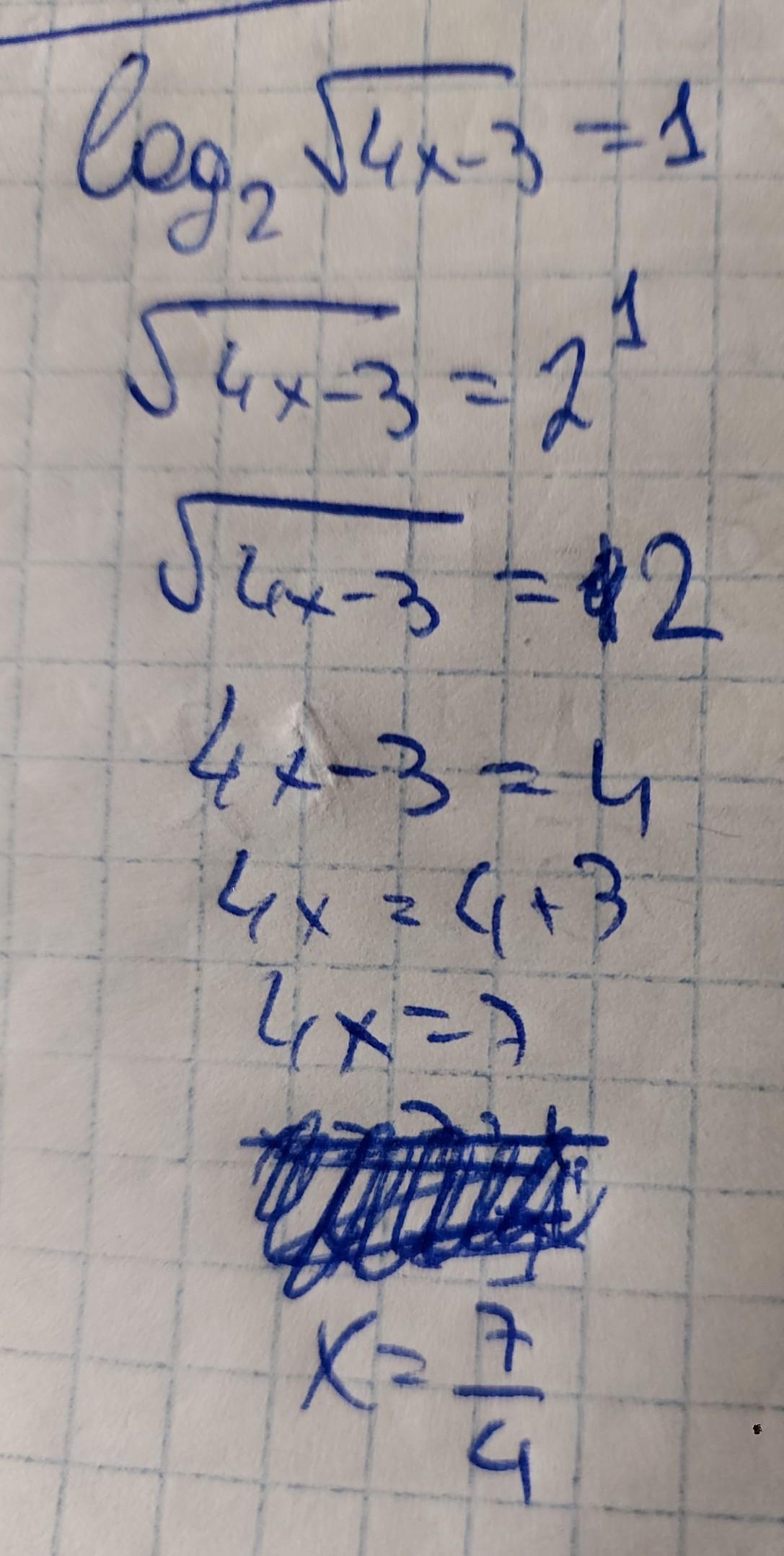
Автор ответа:
0
Найдем ОДЗ:
Правило: ⇒
Возведем обе части уравнения в квадрат ⇒
Корень уравнения удовлетворяет ОДЗ. Проверкой убеждаемся, что корень найден верно.
Ответ: x=1,75.
Похожие вопросы
Предмет: Русский язык,
автор: daliyaasvarova
Предмет: Технология,
автор: ега1940
Предмет: Русский язык,
автор: turgynbaeva
Предмет: Информатика,
автор: ifanakyffu2587
Предмет: Английский язык,
автор: burckowdanil