Предмет: Алгебра,
автор: ssssssami
С объяснением пожалуйста
Если .....то найдите.....
Приложения:
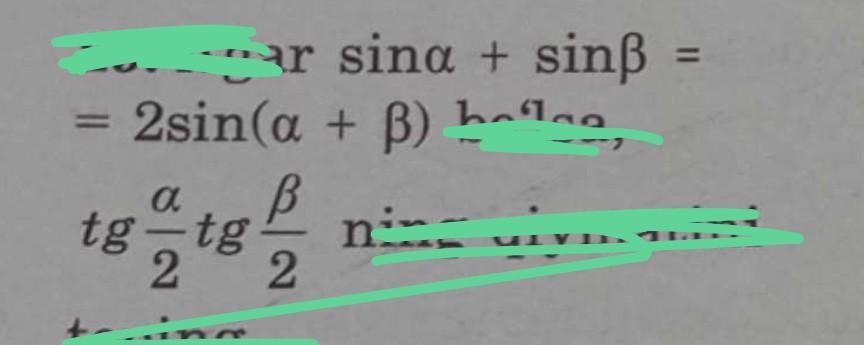
Ответы
Автор ответа:
0
Дано: Нужно узнать, чему равно произведение
Оказывается, ответ можно получить не всегда. Во-первых, тангенсы должны существовать. Это сразу дает ограничение
Во-вторых мы получим в результате работы с условием.
1-й случай.
Поэтому исследуемое выражение может принимать все неположительные значения.
2-й случай.
Вывод: учитель скорее всего просто имел в виду ответ 1/3. Но первый случай забывать нельзя.
Похожие вопросы
Предмет: Русский язык,
автор: roshubin1
Предмет: Русский язык,
автор: 7start7
Предмет: Русский язык,
автор: слава505
Предмет: Физика,
автор: sasha3138
Предмет: Алгебра,
автор: marner93