помогите пожалуйста срочно!!!
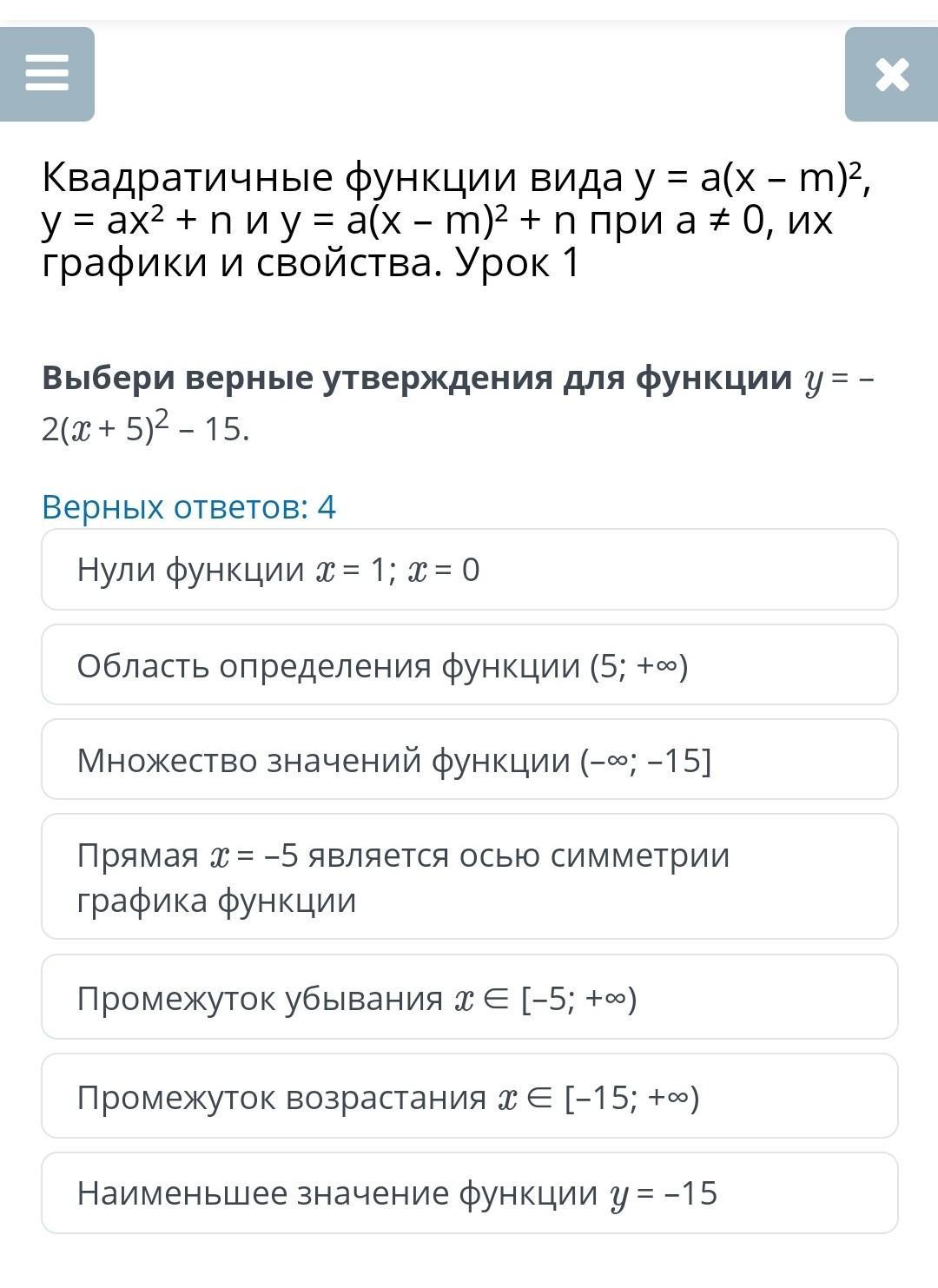
Ответы
Ответ:
1) нули функции х=0, тогда у=65
3) множество значений функции (–∞; –15]
4) прямая х= –5 является осью симметрии функции;
5) промежуток убывания х ∈ [–5; +∞)
Объяснение:
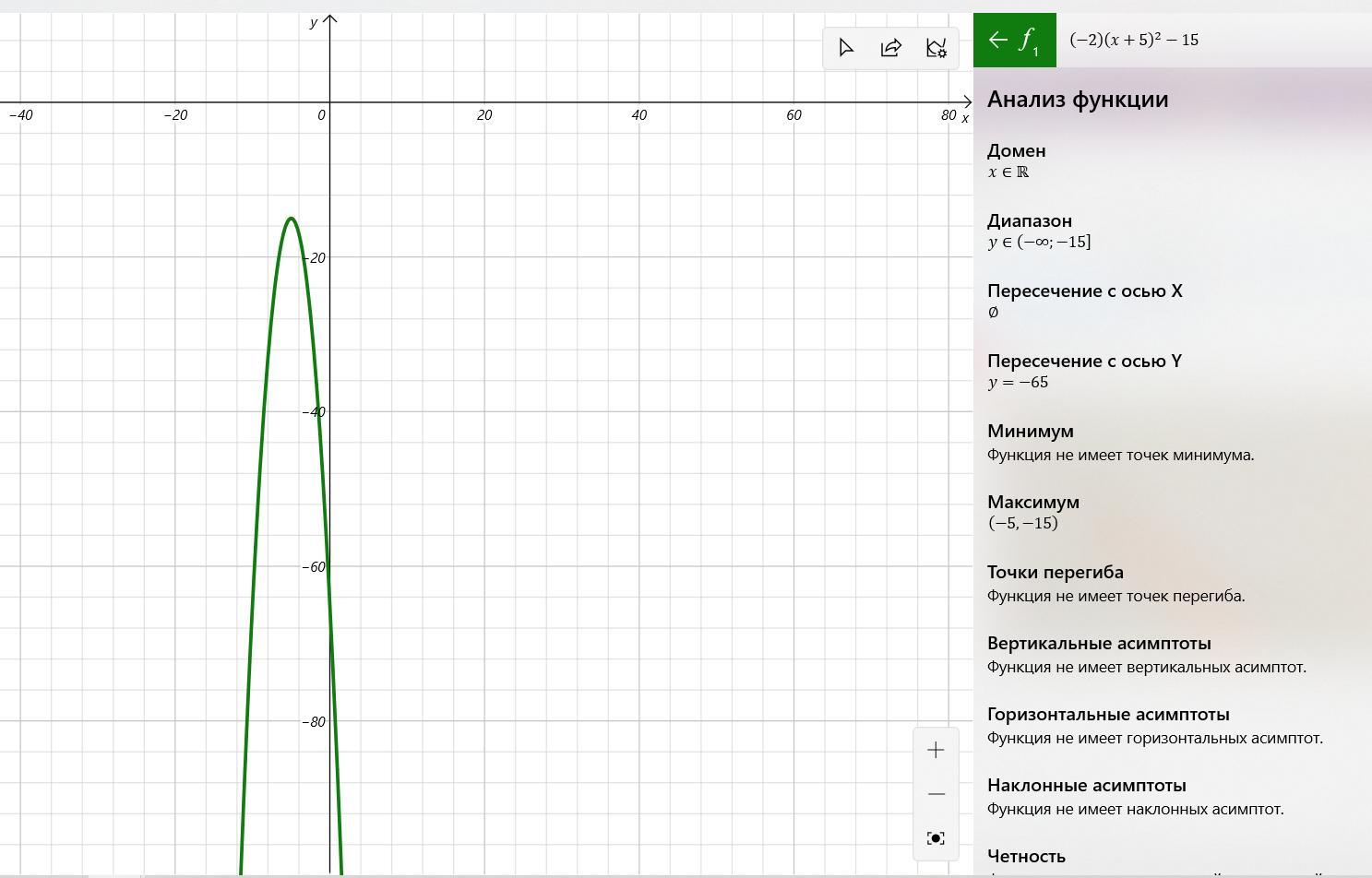
у= –2(х+5)²–15
1) Нули функции означают, что функция имеет пересечения с осями координат х и у.
Сначала найдём точки пересечения с осью х, при этом у=0, решим уравнение, приравняем формулу к 0:
–2(х+5)²–15=0, раскроем скобки:
–2(х²+10х+25)–15=0
–2х²–20х–50–15=0
–2х²–20х–65=0 |×(–1)
2x²+20x+65=0
a=2; b=20; c=65
Д=b²–4ab=20²–4×2×65=400–520= –120
Д < 0, поэтому пересечений с осью х функция не имеет. Теперь проверим есть ли пересечение функции с осью у, при этом х=0, подставим значение х=0 в уравнение функции:
2x²+20x+65=2×0²+20×0+65=0+0+65=65.
Значит функция пересекает ось у=65, при этом х=0, ДА, верно.
2) найдём вершину параболы, используя уравнение 2х²+20х+65 из уравнения в первом пункте. Координату х₀ найдём по формуле:
х₀= –b/2a= –20/2×2= –20/4= –5;
х₀= –5 – она также является уравнением оси симметрии функции. Cлагаемое за скобками (–15) – это у₀ – вершины параболы, координаты её вершины
(х₀; у₀) =(–5; –15).
Учитывая, что перед функцией стоит знак минус, то парабола направлена ветками вниз и координаты вершины параболы является ее максимумом. Тогда область определения функции:
х ∈ R (–∞; +∞)
Утверждение во втором пункте НЕверно.
3) Область значений функции определяется по оси у. Так как высшая точка у= –15 (координата вершины параболы), то область значений функции:
Е(у) = (–∞; –15]
4) ДА, верно, так как осью симметрии функции является координата X вершины параболы
x= –5
5) ДА, верно, функция убывает на промежутке
х∈ [–5; +∞)
6) Неверно, так как функция возрастает на промежутке х ∈ (–∞; –5]
7) НЕверно, так как у= –15 – это максимум функции, то есть принимает наибольшее значение