Предмет: Геометрия,
автор: Аноним
помогите пожалуйста, 8 класс, второй и третий признак подобия треугольников
Приложения:
Reideen:
S=24
можно решение? пожалуйста
Ответы
Автор ответа:
1
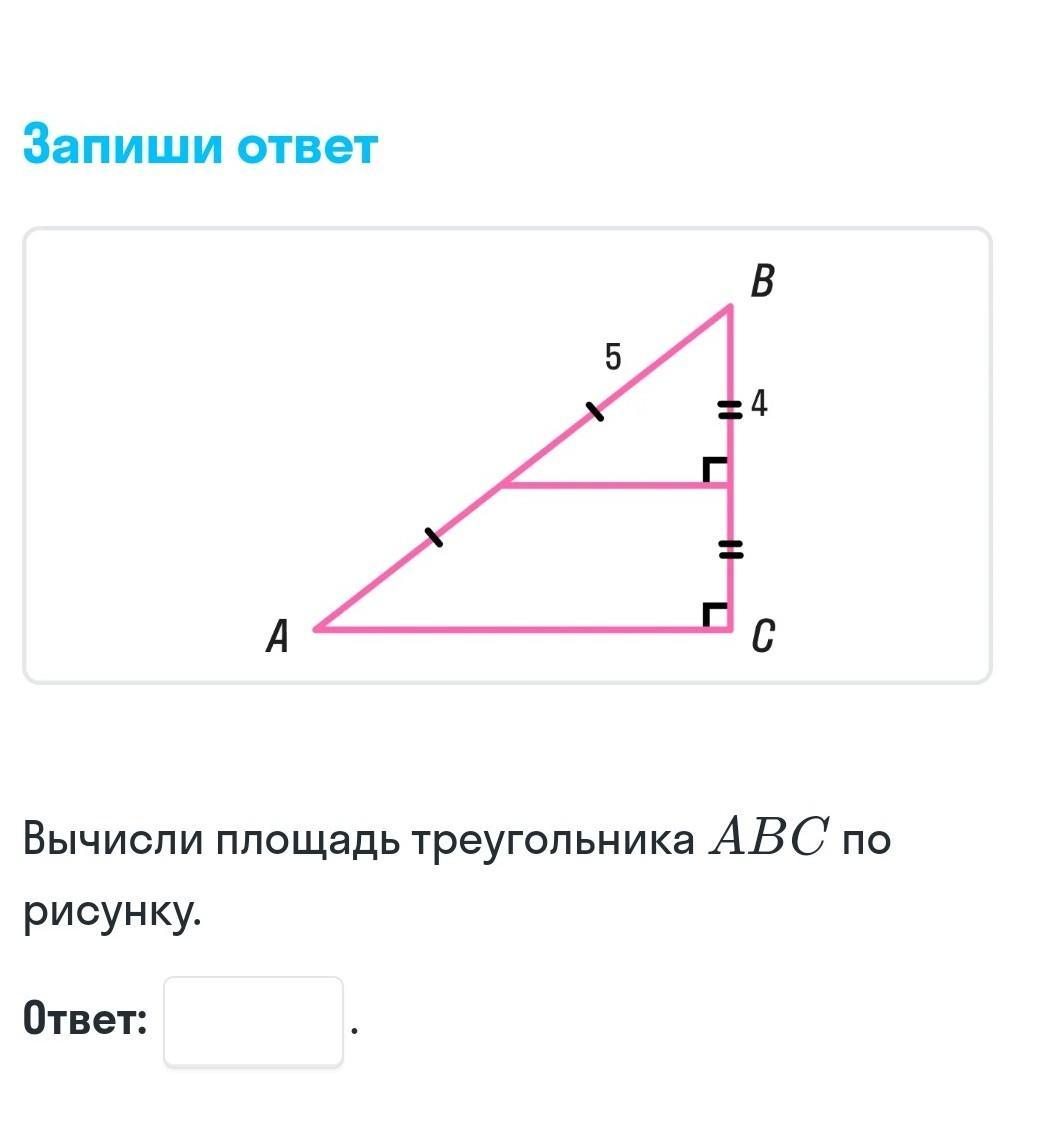
Условно назовем точку пересечения средней линии со стороной AB точкой N, а точку пересечения со стороной BC - точкой M.
1 способ.
Поскольку AN=NB=5, то AB=AN+NB=5+5=10; и если BM=MC=4, то BC=BM+MC=4+4=8.
ΔABC - прямоугольный (∠C=90°), тогда из т. Пифагора:
.
кв. ед.
2 способ.
ΔBMN - прямоугольный (∠NMB=90°).
MN=3, т.к. ΔBMN - египетский.
Поскольку MN параллельна AC и, пересекая стороны AB и BC, делит их на равные отрезки, то MN - средняя линия.
Значит AC=2MN=2·3=6.
кв.ед.
Ответ: S=24.
ну, давайте
Похожие вопросы
Предмет: Русский язык,
автор: Mashe4kaMil
Предмет: Другие предметы,
автор: lexsn
Предмет: Английский язык,
автор: rrr506
Предмет: Математика,
автор: gooo47
Предмет: Математика,
автор: liliya97124