Предмет: Математика,
автор: ap1702009
1.
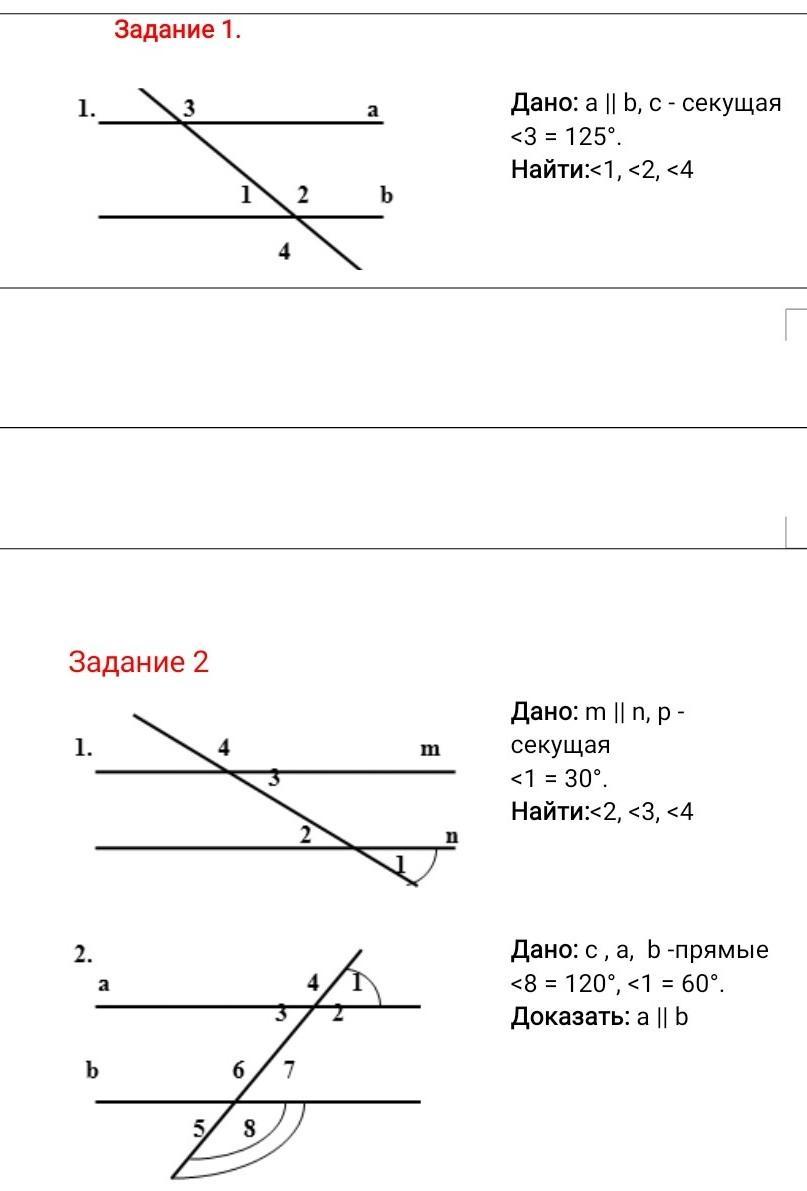
Дано: a || b, c - секущая
<3 = 125°.
Найти:<1, <2, <4
2.
Дано: m || n, p - секущая
<1 = 30°.
Найти:<2, <3, <4
Дано: c , a, b -прямые
<8 = 120°, <1 = 60°.
Доказать: a || b
Помогите пожалуйста!!!
(пожалуйста, укажите доказательства и решения!)
Приложения:
Ответы
Автор ответа:
3
Ответ:
№1
Дано:
a || b, c - секущая
<3 = 125°
Найти:<1, <2, <4
Решение:
∡2 и ∡3 - соответственные(соответственные углы равны)
Значит ∡2=125°;
∡2 и ∡4 - вертикальные(вертикальные углы равны)
Значит ∡4=125°;
∡2 и ∡1 (смежные 180°)
∡1=180-∡2=180-125=55°.
№2
Дано: m || n, p - секущая
<1 = 30°.
Найти:<2, <3, <4
Решение:
∡1 и ∡2 - вертикальные (вертикальные углы равны)
Значит ∡2=30°;
∡1 и ∡3 - соответственные (соответственные углы равны)
Значит ∡3=30°
∡4=180-∡3=180-30=150°.
№3
Дано: c , a, b -прямые
<8 = 120°, <1 = 60°.
Доказать: a || b
Решение:
∡8 и ∡1 - внешние односторонние.
Теорема:
Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
120+60=180° ⇒ a ║ b.
Пошаговое объяснение:
ap1702009:
спасибо большое!
не за что
а как поставить "лучший ответ", просто кнопка не отображается
Похожие вопросы
Предмет: Английский язык,
автор: ррр207
Предмет: Русский язык,
автор: лесенька2
Предмет: Английский язык,
автор: одд2
Предмет: Биология,
автор: MAPKEP
Предмет: Химия,
автор: Disonium1