Предмет: Алгебра,
автор: nilipoop5
ПОМОГИТЕ ПОЖАЛУЙСТА, СРОЧНО!
Приложения:
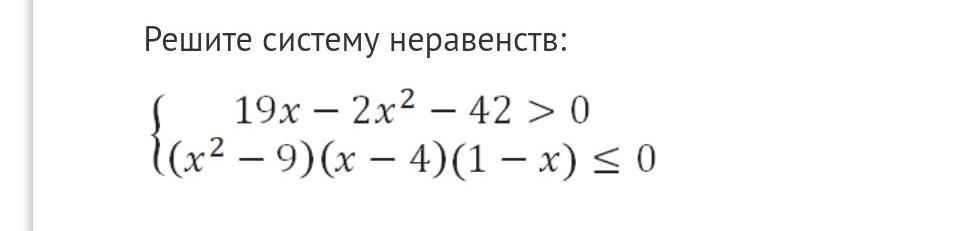
Ответы
Автор ответа:
0
+ + + + + (3,5) - - - - - (6) + + + + +
////////////
+ + + + + [- 3] - - - - - [1] + + + + + [3] - - - - - [4] + + + + +
//////////////// ////////////////// ////////////////
Похожие вопросы
Предмет: Русский язык,
автор: PrincessArina
Предмет: Русский язык,
автор: Котэ1121
Предмет: Русский язык,
автор: evgeniysavcenk
Предмет: Английский язык,
автор: Diko11111111111
Предмет: Химия,
автор: mashaonelove2002