Предмет: Математика,
автор: 59182eva
помните пожалуйста. срочно. производная
Приложения:
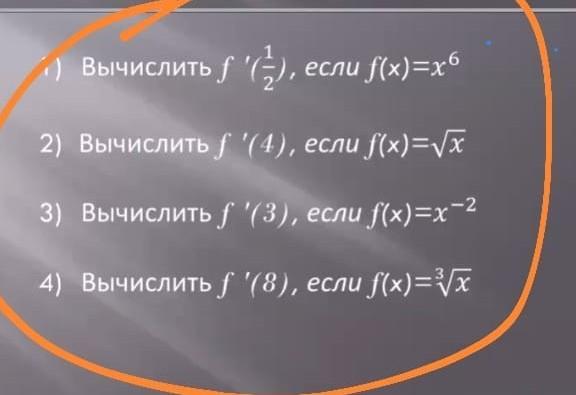
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Английский язык,
автор: sasha17052005
Предмет: Русский язык,
автор: Yana1231111
Предмет: Қазақ тiлi,
автор: masafaca
Предмет: Алгебра,
автор: loser666685yd6r5d
Предмет: Уход за собой,
автор: Rexona2018