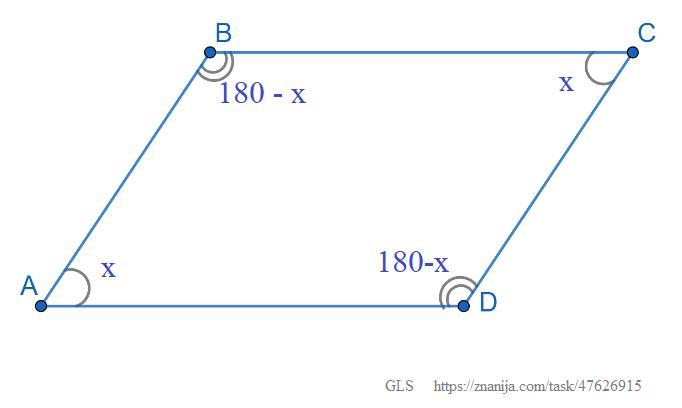
Сумма двух углов параллелограмма на 18◦ больше третьего угла этого паралле- лограмма. Чему может быть равен меньший угол в этом параллелограмме? [Укажите все возможные ответы]
Ответы
Ответ:
Меньший угол параллелограмма 18° или 66°.
Объяснение:
Определить меньший угол параллелограмма, если известно, что сумма двух из них больше третьего угла.
Дано: ABCD - параллелограмм; сумма двух углов его на 18° больше третьего угла.
Найти: углы параллелограмма.
Решение.
- Параллелограмм - это четырехугольник, у которого противоположные стороны попарно параллельны.
- В параллелограмме противолежащие углы равны.
1) Рассмотрим параллелограмм ABCD.
Сумма двух углов параллелограмма, прилежащих к одной стороне, равна 180°, так как они являются односторонними углами при параллельных прямых BC и AD и секущей AB.
∠A + ∠B = 180°.
Для удобства, обозначим один из углов параллелограмма переменной x°, тогда другой равен 180° - x°.
2) Допустим два равных угла больше на 18° третьего угла.
По условию составим уравнение.
2x = 180 - x + 18;
3x = 198;
x = 198 : 3;
x = 66.
Острые углы параллелограмма 66°, тупые углы 180° - 66° = 114°.
Проверка.
2·66° - 114° = 132° - 114° = 18° Верно.
3) Допустим два разных угла (то есть прилежащих к одной стороне параллелограмма) больше третьего на 18°.
Сумма двух углов параллелограмма, прилежащих к одной стороне равна 180°
180 = x + 18.
x =180 - 18;
x = 162;
Один из углов 162°, а другой 180° - 162° = 18° для углов, прилежащих к одной стороне.
Проверка:
Сумма двух углов 162° + 18° = 180°
180° больше, чем угол 162° на 18°.
Верно.
Меньший угол параллелограмма может быть 18° или 66°.