Пытаюсь решить немонотонную функцию уже целый день. Без вашей помощи не справлюсь к сожалению.
Ответы
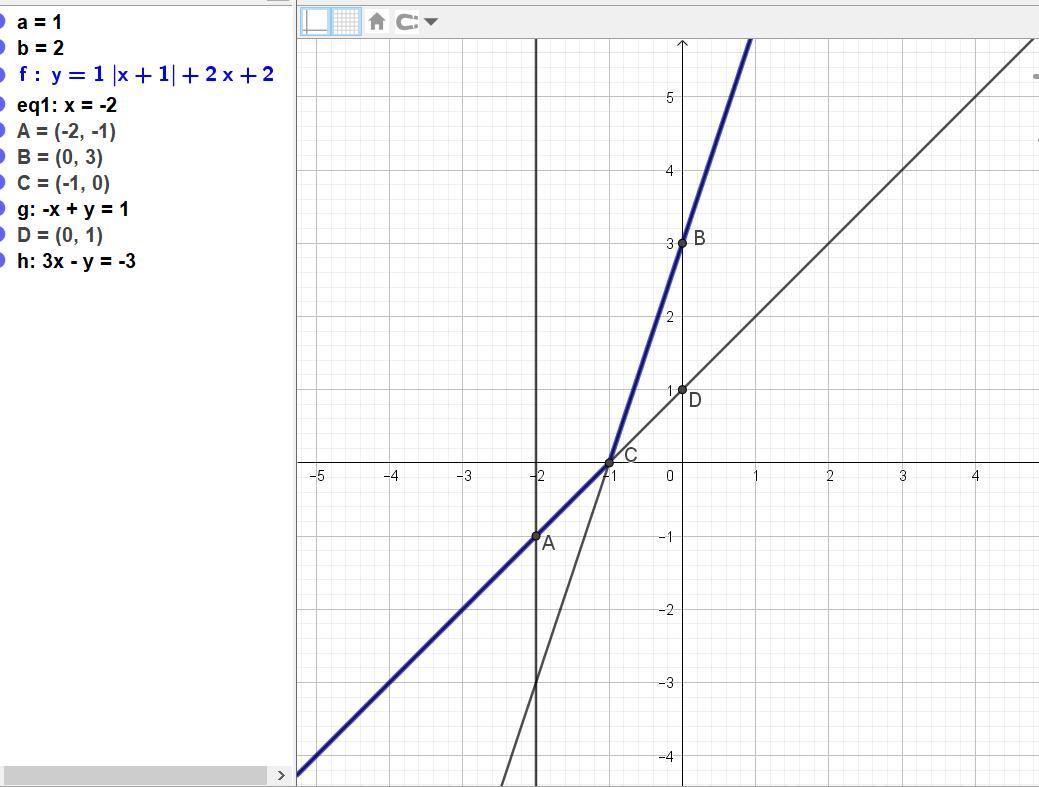
Так как в заданном уравнении есть модуль, то заданную функцию f(x) = a|x + 1| + bx + 2 разделим на две по свойству модуля.
Первое значение при положительных знаках в модуле.
f(x)1 = ax + a + bx + 2, сгруппируем: f(x)1 = (a + b)x + (a + 2).
Получена линейная функция вида у = кx + b.
В ней свободный член "b" соответствует точке пересечения графика оси Оу при х = 0. А это правая точка заданного промежутка, где функция равна 3.
Приравняем а + 2 = 3, отсюда а = 3 - 2 = 1.
Найдено значение параметра а = 1.
Теперь переходим ко второму варианту знаков выражения в модуле.
Второе значение при отрицательных знаках в модуле.
f(x)2 = -ax - a + bx + 2, сгруппируем: f(x)2 = (b - a)x + (-a + 2).
Используем левую границу заданного промежутка.
Параметр а найден и равен 1, поэтому подставим значение функции "-1" в точке х = -2 в функцию f(x)2 = (b - a)x + (-a + 2).
-1 = (b - 1)*(-2) + (-1 + 2),
-1 = -2b + 2 + 1,
2b = 4, отсюда находим b = 4/2 = 2.
Ответ: a = 1, b = 2.