Предмет: Математика,
автор: Аноним
Вычислить производные, помогите пожалуйста
Приложения:
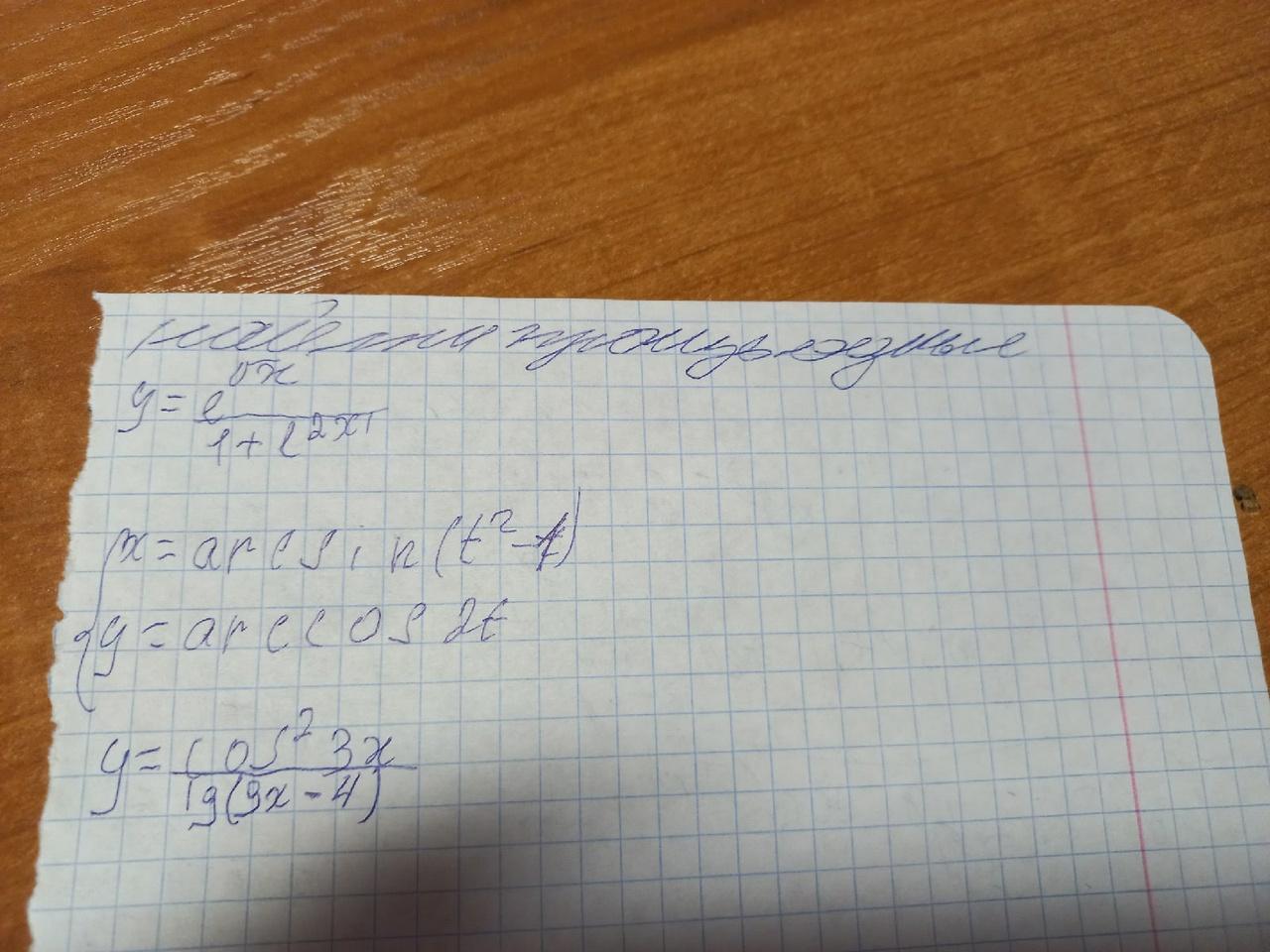
natalyabryukhova:
в первом примере в знаменателе е в какой степени?
корень из икс
Я про знаменатель?)
2 икс штрих
Уже решила, как поняла.
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
1.
Производная частного:
Производная сложной функции:
2.
Производная функции, заданной параметрически:
Дано:
3.
Здесь производная частного.
Использовали формулы производных сложных функций:
Приложения:

Похожие вопросы
Предмет: Қазақ тiлi,
автор: НастяКсор
Предмет: Українська мова,
автор: KseniaMamaeva
Предмет: Английский язык,
автор: Pashka5555
Предмет: Геометрия,
автор: lramaldanova
Предмет: Қазақ тiлi,
автор: zxcv27