Предмет: Математика,
автор: bb573878
решите систему уравнений
Приложения:
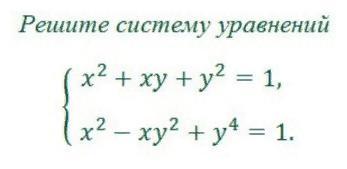
Ответы
Автор ответа:
6
Ответ:
(см. объяснение)
Пошаговое объяснение:
Тогда либо , либо
, либо
.
В первых двух случаях очевидно, что:
В последнем случае при получим:
Отсюда либо (тогда
), либо
.
Последнее уравнение имеет один корень и решается по формуле Кардано.
Осталось посчитать :
Теперь осталось аккуратно записать ответ:
Система уравнений решена!
Аноним:
Здорово)) С НГ!
MrSolution, а Вы не могли бы об'яснить как нашли корень методом Кардано
Похожие вопросы
Предмет: Русский язык,
автор: влад979
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: chyngyz69
Предмет: Литература,
автор: rertgdd