(Даю 100 баллов за решение)
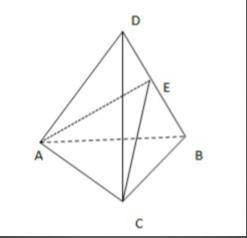
Вершины пирамиды находятся в точках A,В,С,D
Вычислить:
1) угол AC,AB между указанными рёбрами
2) Площадь сечения проходящего через середину ребра BD и две вершины пирамиды
3) Объем пирамиды ABCD
A=(5,2,4)
B= (-3,-4,4)
C= (1,-5,8)
D= (9,-3,5)
Ответы
Вершины пирамиды находятся в точках:
A(5; 2; 4), B(-3; -4; 4), C(1; -5; 8), D(9; -3; 5).
Вычислить:
1) угол AC,AB между указанными рёбрами.
Находим векторы АС и АВ и их модули
АС = C(1; -5; 8) - A(5; 2; 4) = (-4; -7; 4),
|AC| = √((-4)² + (-7)² + 4²) = √(16 + 49 + 16) = √81 = 9.
АB = B(-3; -4; 4) - A(5; 2; 4) = (-8; -6; 0),
|AB| = √((-8)² + (-6)² + 0²) = √(64 + 36 + 0) = √100 = 10.
Косинус угла равен:
cos(AC_AB) = ((-4)*(-8)+(-7)*(-6)+4*0)/(9*10) = (32+42+0)/90 = 74/90 = 37/45.
Угол равен arccos(37/45) = 0,6055 радиан или 34,6921 градуса.
2) Площадь сечения проходящего через середину ребра BD (точка Е) и две вершины пирамиды (А и С).
Заданное сечение АЕС, его площадь находим как половину модуля векторного произведения векторов АЕ и СЕ.
Находим координаты точки Е как середины ребра BD.
Е = (B(-3; -4; 4) + D(9; -3; 5))/2 = (3; -3,5; 4,5).
Теперь определяем векторы АЕ и СЕ.
АЕ = Е(3; -3,5; 4,5) - A(5; 2; 4) = (-2; -5,5; 0,5),
СЕ = Е(3; -3,5; 4,5) - С(1; -5; 8) = (2; 1,5; -3,5).
Векторное произведение по схеме Саррюса равно:
I j k| I j
-2 -5,5 0,5| -2 -5,5
2 1,5 -3,5| 2 1,5 = 19,25i + 1j – 3k – 7j – 0,75i + 11k = 18,5i – 6j + 8k
Вектор как произведение AE и CE равен (18,5; -6; 8).
Находим площадь S.
S = (1/2)√(18,5² + (-6)² + 8²) = (1/2)√(342.25 + 36 + 64) = (1/2)√442,5 ≈ 10,515.
3) Объем пирамиды ABCD.
Объем пирамиды равен (1/6) смешанного произведения векторов АВ, АС и AD. Векторы АВ и АС найдены и равны:
АB = (-8; -6; 0),
АС = (-4; -7; 4),
АD = D(9; -3; 5) - A(5; 2; 4) = (4; -5; 1).
Произведение равно:
-8 -6 0| -8 -6
-4 -7 4| -4 -7
4 -5 1| 4 -5 = 56 – 96 + 0 – 24 – 160 – 0 = -224.
V = (1/6)*|-224| = 224/6 = 112/3 ≈ 37,333.