Предмет: Алгебра,
автор: nikitanikolenko10
даю 85 балов!!!
смотри фото:
Приложения:


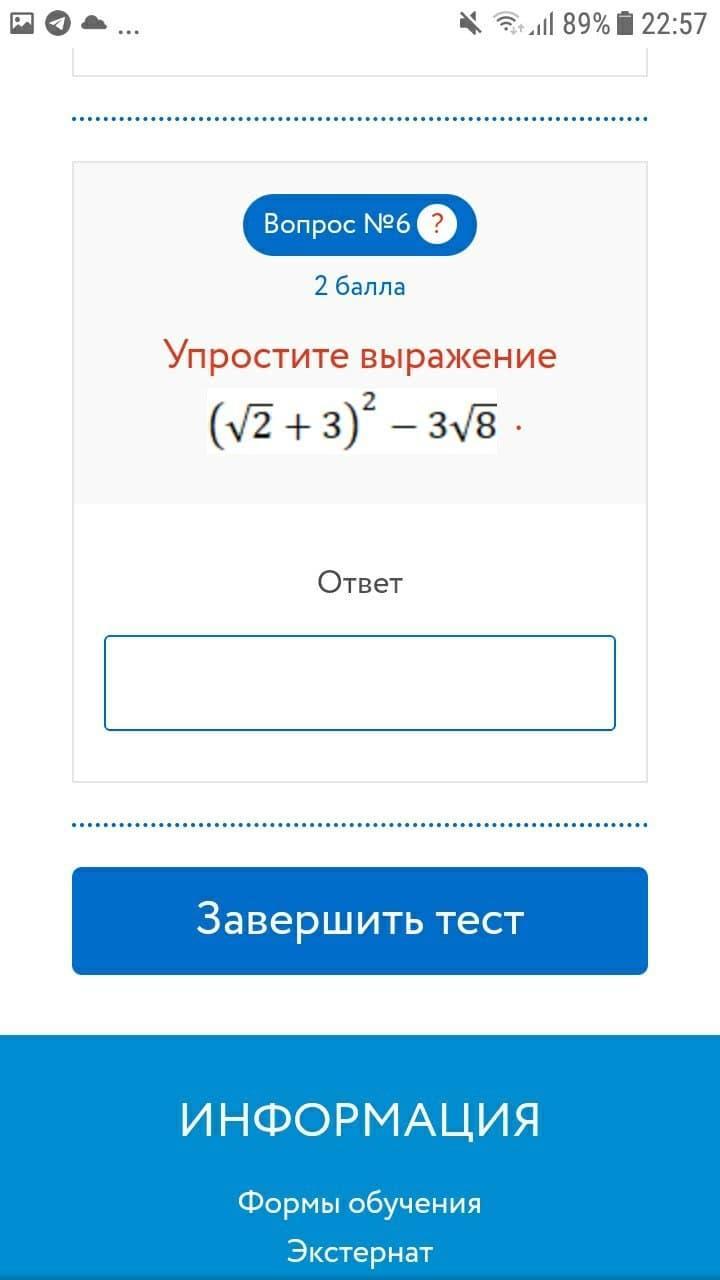
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Українська мова,
автор: Христинка2912
Предмет: Русский язык,
автор: 54677889999010
Предмет: Русский язык,
автор: март55
Предмет: Русский язык,
автор: solodkovtrifon
Предмет: Математика,
автор: nazerkeormanbek