Предмет: Алгебра,
автор: ikssa
Помогите пожалуйста решить.
Найти предел, не пользуясь правилом Лопиталя.
Приложения:
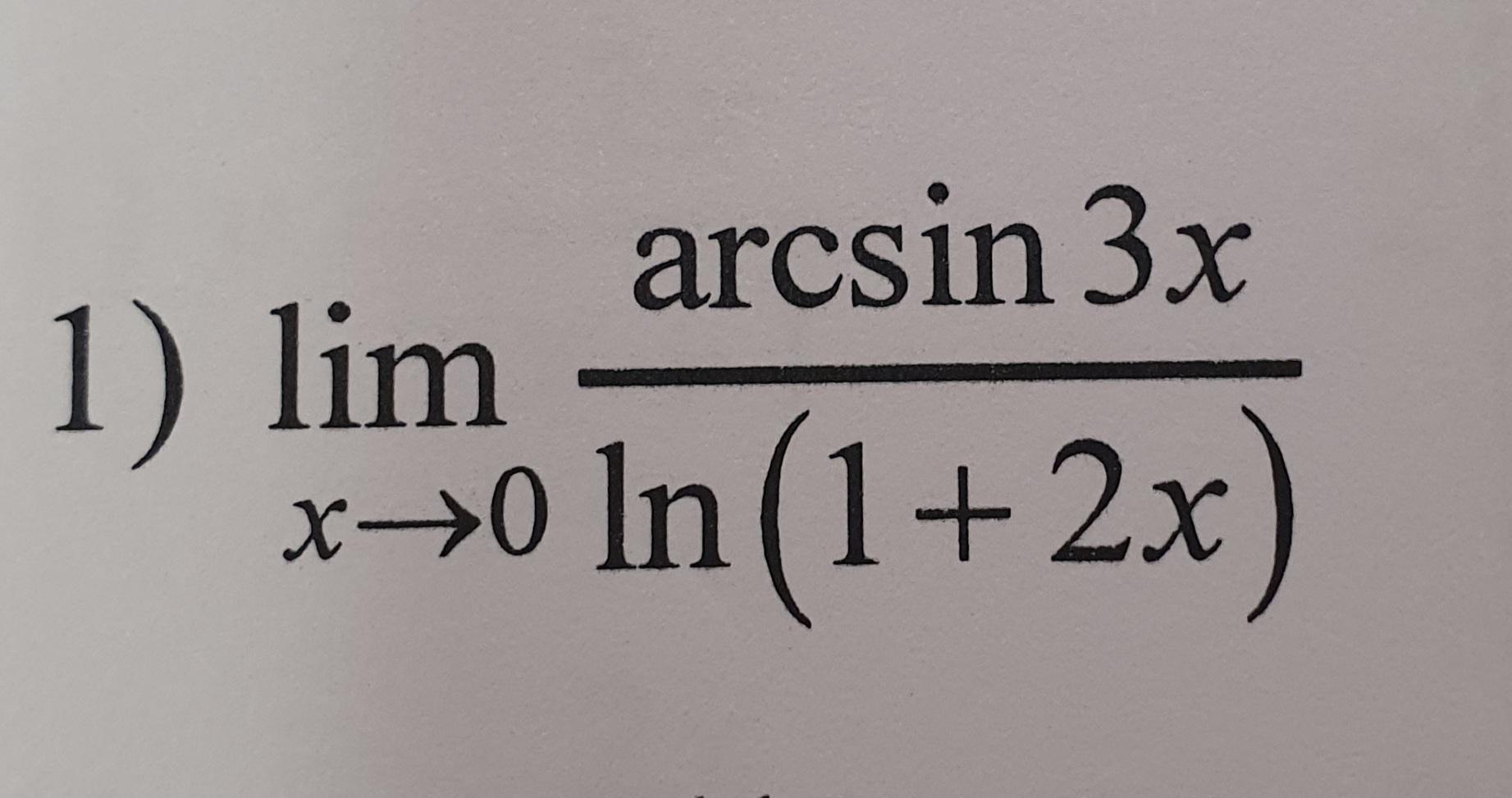
Ответы
Автор ответа:
0
lim x*[ln(3x-1)-ln(3x-2)]=x*ln((3x-1)/(3x-2))=
x*ln(1+1/(3x-2))
из 3-го замечательного предела ln((1+t))/t=1 при t-->0 следует что ln(1+t) эквивалентно t, поэтому заменяем ln(1+1/(3x-2)) на 1/(3x-2) и получим
lim(x/(3x-2)) далее делим числитель и знаменатель на Х и получим
lim(1/(3-2/.х) ) =1/3
хз может помог
Автор ответа:
1
докажем сначала, что
arcsin(y) эквивалентно y, при y -> 0, и
ln(1+y) эквивалентно y, при y -> 0.
lim arcsin(y)/y = [ t = arcsin(y), тогда sin(t) = y, t -> 0] = lim t/sin(t) = 1.
lim ln(1+y)/y = lim ln(1+y)^(1/y) = ln( lim (1+y)^(1/y) ) = ln e = 1.
При x -> 0, имеем 3x ->0 и 2x ->0.
Поэтому имеем
lim arcsin(3x)/ln(1+2x) = lim 3x/2x = 3/2 = 1,5
Похожие вопросы
Предмет: Русский язык,
автор: алинаазизова1
Предмет: Немецкий язык,
автор: 288305709
Предмет: Қазақ тiлi,
автор: marijuana85
Предмет: Химия,
автор: Derispe
Предмет: Русский язык,
автор: darinavolovik