Предмет: Алгебра,
автор: Лолкекчебурек1337
Решите систему неравенств.
Приложения:
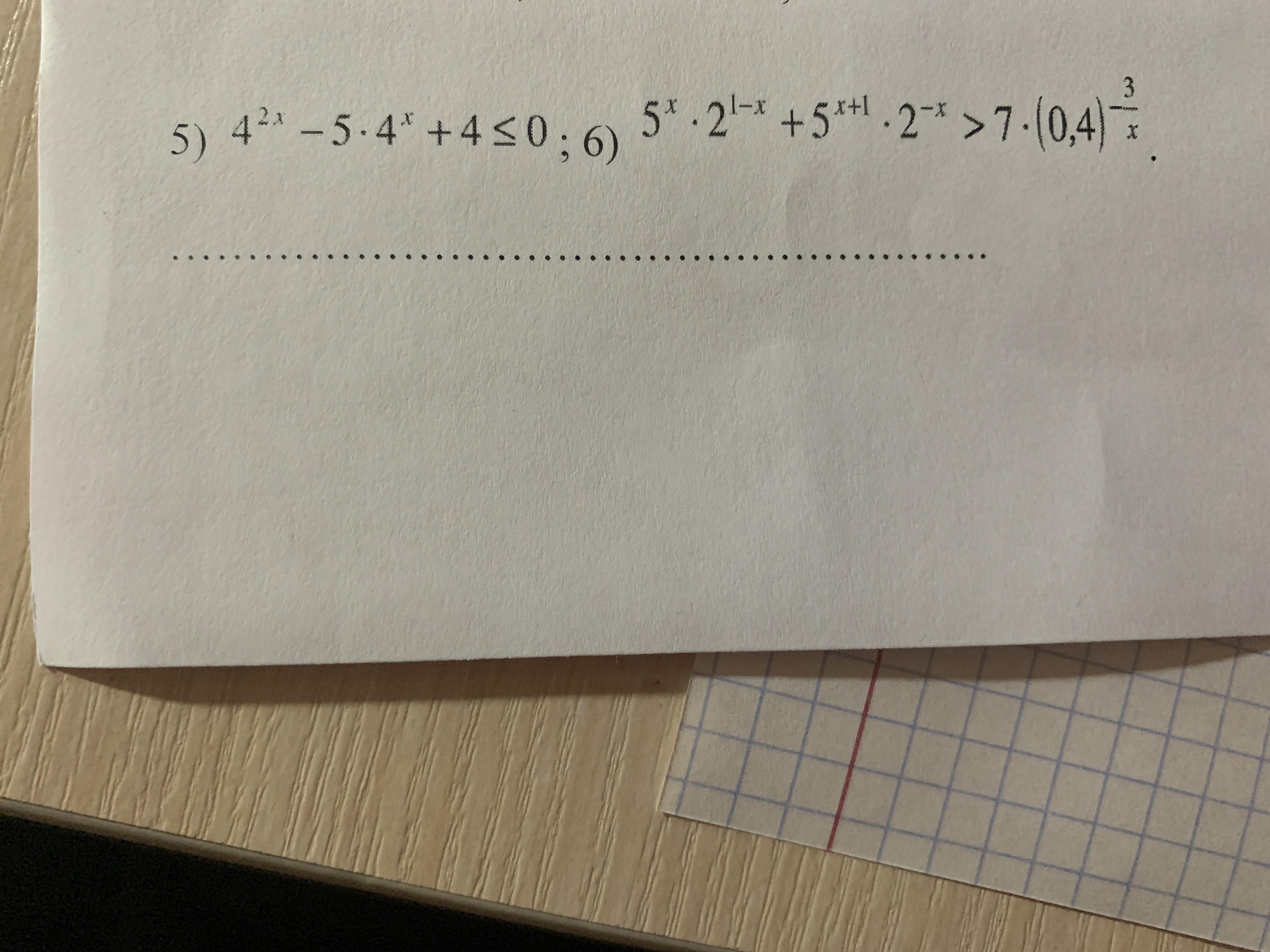
Universalka:
Здесь нет ни одной системы неравенств
Ответы
Автор ответа:
1
+ + + + + [1] - - - - - [4] + + + + + m
////////////////
m ∈ [1 , 4]
- - - - - (-√3) + + + + + (0) - - - - - (√3) + + + + +
/////////////// /////////////
Ответ : x ∈ (- √3 ; 0) ∪ (√3 ; +∞)
Похожие вопросы
Предмет: Русский язык,
автор: nastdjvcd
Предмет: Қазақ тiлi,
автор: arslan2825
Предмет: Русский язык,
автор: иваннне
Предмет: Алгебра,
автор: матросскин
Предмет: Литература,
автор: tavtorkina2016