Предмет: Геометрия,
автор: Ансар1337
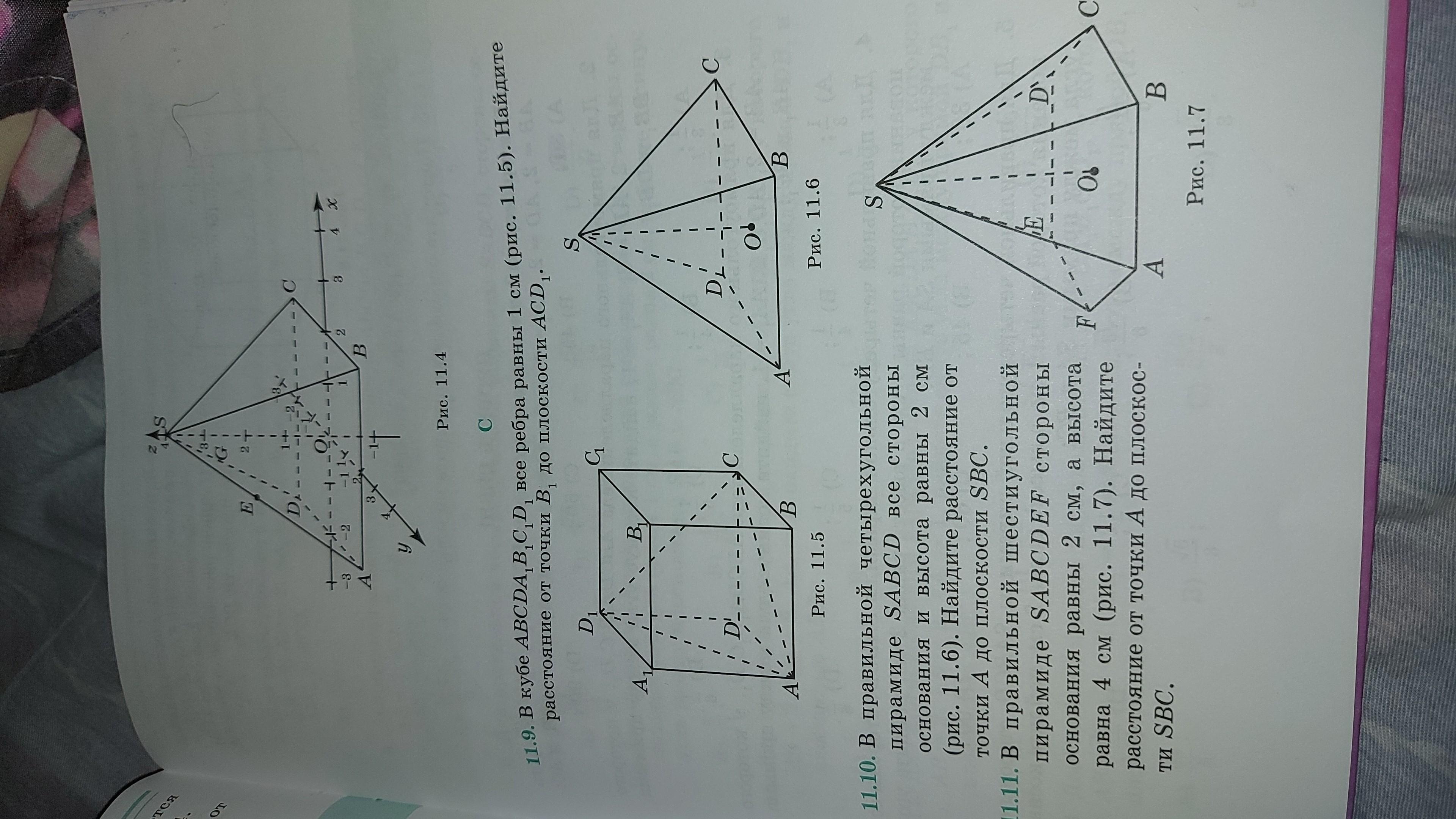
Помогите решить 11.9 пожалуйста
Приложения:
Ответы
Автор ответа:
1
В основании квадрат, диагонали квадрата перпендикулярны, BD⊥AC.
BD⊥AC, BB1⊥(ABC) => B1D⊥AC (теорема о трех перпендикулярах)
Аналогично B1D⊥AD1, следовательно B1D⊥(ACD1)
B1H - искомое расстояние.
Рассмотрим пирамиду DACD1.
V = 1/3 S(ACD1) DH = 1/3 S(ACD) DD1
S(ACD1) =1/2 *AC^2 sin60 =√3/2
S(ACD) =1/2
=> √3/2 *DH =1/2 => DH=√3/3
Диагональ единичного куба √3.
B1H =B1D-DH =√3 - √3/3 =2√3/3
Проверим. H - центр ACD1 по построению, пересечение медиан. O - середина BD. Проекция H делит DO 2:1 и DB 1:2 => H делит DB1 1:2 => B1H=2/3 *√3
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: Анютка012a
Предмет: Русский язык,
автор: olezhka2006
Предмет: Русский язык,
автор: alief12
Предмет: Русский язык,
автор: nastysha70
Предмет: Английский язык,
автор: Нюша11112