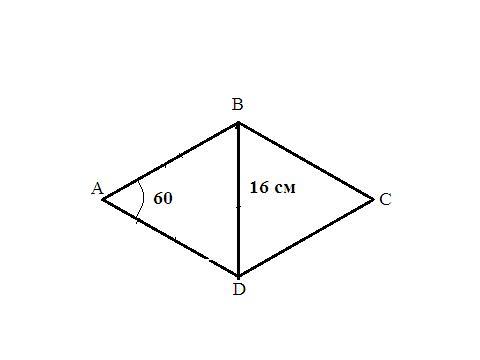
Разность двух углов ромба равна 60°. Меньшая диагональ ромба равна 16 см. Найдите периметр ромба.
очень срочно! помогите пожалуйста, даю 90 баллов

Ответы
Так как Abcd- ромб, зн. Ао=ос,во=оd,Ab=bc=cd=da. Когда разность двух углов ромба равна 60°,значит угол А- угол В=60°.Возьмем через х неизвестный угол. А тогда большой угол будет 2х.Сделаем уравнения:
2х-х=60
Х=60
Тогда 2х=120°.Рассмотрим треугольник АВО.Угол ВАО=60°
Угол АВО=30°
Угол АОВ=90°
Мы знаем, что катет, который лежит напротив угла в 30° равен Одну вторую гипотенузы. Значит Ав=2АО=16см.
Равсd=16*4=64cм
Ответ:
Объяснение:
Один угол - х, другой угол у;
система уравнений:
х-у=60
х+у=180
решаем методом сложения:
2х=240
х=120°
у=180-120=60°;
стороны ромба и его меньшая диагональ образуют равнобедренный треугольник со сторонами - стороны ромба и основанием - меньшая диагональ. Углы при основании равны:
(180-60)/2=60° ⇒ треугольник равносторонний со стороной 16 см ⇒
периметр ромба = Р=16*4=64 см.