Предмет: Алгебра,
автор: Аноним
Исследовать числовой ряд на сходимость.
Приложения:
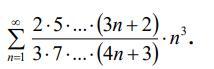
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: 56812345
Предмет: Окружающий мир,
автор: alisakhv
Предмет: Английский язык,
автор: Аноним
Предмет: Геометрия,
автор: kiril000601
Предмет: Литература,
автор: dashacat89399393
можешь тут помочь, пожалуйста!
https://znanija.com/task/46625052