Question

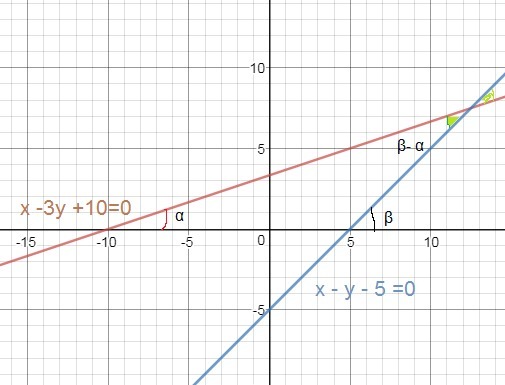
Найти угол между прямыми х-3у+10=0 и x-y-5=0

Answer 1

x-3y+10=0   ⇒  y=(1/3)x+(10/3)⇒   k₁=1/3 ⇒  tgα=1/3

α - угол, который образует прямая x-3y+10=0  с положительным направлением оси Ох;

x-y-5=0  ⇒ y=x-5 ⇒   k₂=1⇒  tgβ=1

β - угол, который образует прямая x-y-10=0  с положительным направлением оси Ох;

Тогда угол между прямыми равен (β-α)

tg(β-α)=(tgβ-tgα)/(1+tgβ·tgα)=(1-(1/3))/(1+(1/3))=(2/3)/(4/3)=1/2

О т в е т. β-α= arctg(1/2)